题目内容
经过点(2,-3)且与椭圆9x2+y2=36共焦点的椭圆方程为 .
考点:椭圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:先计算椭圆9x2+y2=36的焦点坐标,发现所求椭圆焦点在y轴上,再用待定系数法设出所求椭圆方程,最后将点(2,-3)代入即可.
解答:
解:∵椭圆9x2+y2=36的标准方程为
+
=1
∴其焦点坐标为(0,±4
)
∵所求椭圆与椭圆9x2+4y2=36有相同的焦点,
∴设所求椭圆方程为
+
=1(m>0)
∵椭圆经过点(2,-3)
∴
+
=1
∴m=
∴和椭圆9x2+y2=36有相同的焦点,且经过点(2,-3)的椭圆的方程为
+
=1.
故答案为:
+
=1.
| x2 |
| 4 |
| y2 |
| 36 |
∴其焦点坐标为(0,±4
| 2 |
∵所求椭圆与椭圆9x2+4y2=36有相同的焦点,
∴设所求椭圆方程为
| x2 |
| m |
| y2 |
| m+32 |
∵椭圆经过点(2,-3)
∴
| 4 |
| m |
| 9 |
| m+32 |
∴m=
| ||
| 2 |
∴和椭圆9x2+y2=36有相同的焦点,且经过点(2,-3)的椭圆的方程为
| x2 | ||||
|
| y2 | ||||
|
故答案为:
| x2 | ||||
|
| y2 | ||||
|
点评:本题考查了椭圆的标准方程及其几何性质,求椭圆的标准方程要先定位,再定量,待定系数法求曲线方程的运用.

练习册系列答案
相关题目
函数h(x)=2sin(2x+
)的图象与函数f(x)的图象关于点(0,1)对称,则函数f(x)可由h(x)经过怎样的变换得到( )
| π |
| 4 |
A、向上平移2个单位,向右平移
| ||
B、向上平移2个单位,向左平移
| ||
C、向下平移2个单位,向右平移
| ||
D、向下平移2个单位,向左平移
|
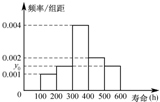 对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如图.
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如图.