题目内容
已知A={x|x2-2x-3＜0}，B={x|（
）x-a≤1}，A∩B=Φ，求实数a的取值范围．
| 1 |
| 2 |
考点：指、对数不等式的解法,交集及其运算
专题：集合
分析：首先化简两个集合，如果依据A∩B=Φ，找到a的范围．
解答：
解：由已知，A=（-1，3），B=[a，+∞），
要使A∩B=Φ，只要a≥3；
所以a的取值范围为a≥3．
要使A∩B=Φ，只要a≥3；
所以a的取值范围为a≥3．
点评：本题考查了集合的化简与运算；化简集合B时注意利用指数函数的单调性．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
若定义运算a*b=
则函数f（x）=3x*3-x的值域是（ ）
|
| A、（0，1] |
| B、[1，+∞） |
| C、（0，+∞） |
| D、（-∞，+∞） |
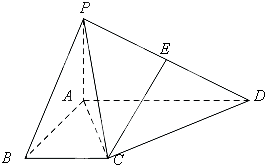如图，四棱锥P-ABCD中，PA⊥平面ABCD，PB与底面所成的角为45°，底面ABCD为直角梯形，∠ABC=∠BAD=90°，AD=2PA=2BC=2．