题目内容
在等比数列{an}中，a7=2a5+a6，则公比q等于（ ）
| A、1 | B、-1 | C、2 | D、2或-1 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：设等比数列{an}的公比为q，利用等比数列的通项公式解出即可．
解答：
解：设等比数列{an}的公比为q，
由a7=2a5+a6，得q2-q-2=0，
解得q=2或q=-1．
故选：D．
由a7=2a5+a6，得q2-q-2=0，
解得q=2或q=-1．
故选：D．
点评：本题考查了等比数列的通项公式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
集合A满足：若a∈A，则
∈A，则满足条件的元素最少的集合A中的元素个数有（ ）
| 1 |
| 1-a |
| A、1 | B、2 | C、3 | D、4 |
设a＞b＞0，且ab=2，则a2+
的最小值是（ ）
| 1 |
| a(a-b) |
| A、1 | B、2 | C、3 | D、4 |
若曲线
（θ为参数），则点（x，y）的轨迹是（ ）
|
| A、直线x+2y-3=0 |
| B、以（2，0）为端点的射线 |
| C、圆（x-1）2+y2=1 |
| D、以（2，0）和（0，1）为端点的线段 |
在△ABC中，角A，B，C所对的边长分别为a，b，c，若sin（A+
）=1且
=
，则∠C等于（ ）
| π |
| 3 |
| b |
| a |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
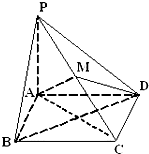如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=1，点M是棱PC上的一点，且AM⊥PB．