Question

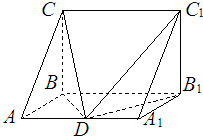如图，在直三棱柱ABC-A₁B₁C₁中，AB⊥BC，BC=

3

，AA₁=2，AB=1，D为AA₁的中点．
（1）求三棱柱的表面积；
（2）求证：平面DBC⊥平面DB₁C₁．

Answer 1

考点：平面与平面垂直的判定,棱柱、棱锥、棱台的侧面积和表面积

专题：空间位置关系与距离

分析：（1）分别求出三个侧面和两个底面的面积相加即可；
（2）利用直三棱柱的性质进一步证明BD⊥平面B₁C₁D，利用面面垂直的性质证明．

解答： （1）解：因为几何体为直三棱柱ABC-A₁B₁C₁中，AB⊥BC，BC=

3

，AA₁=2，AB=1，D为AA₁的中点．
所以AC=2，各侧面都是矩形，各侧面的面积和为2×2+2×1+2×

3

=6+2

3

，两个底面的面积为2×

1

2

×AB×BC=1×

3

=

3

，
所以三棱柱的表面积为6+3

3

；
（2）证明：∵直三棱柱ABC-A₁B₁C₁中，AB⊥BC，BC=

3

，AA₁=2，AB=1，D为AA₁的中点．
∴BB₁=2，BD=B₁D=

2

AB=

2

，
∴BD⊥B₁D，
又AB⊥BC，∴B₁C₁⊥AB，又B₁C₁⊥BB₁，
∴B₁C₁⊥平面ABB₁A₁，
∴B₁C₁⊥BD，
∴BD⊥平面B₁C₁D，
∴平面DBC⊥平面DB₁C₁．

点评：本题考查了三棱柱的表面积求法以及面面垂直的判定，关键是明确直三棱柱的性质，运用性质创造面面垂直的条件．