题目内容
已知
=(3,2),
=(-1,1),向量
与3
-2
平行,|
|=4
,求向量
的坐标.
| a |
| b |
| m |
| a |
| b |
| m |
| 137 |
| m |
考点:平面向量的坐标运算
专题:平面向量及应用
分析:根据向量的坐标运算,以及向量的平行的条件,以及向量的模,即可求出坐标
解答:
解:设向量
的坐标为(x,y),
∵
=(3,2),
=(-1,1),
∴3
-2
=3(3,2)-2(-1,1)=(9,6)-(-2,2)=(11,4),
∵向量
与3
-2
平行,
∴4x=11y,①
∵|
|=4
,
∴x2+y2=4×137②
由①②解得
或
故向量
的坐标为(22,8),或(-22,-8)
| m |
∵
| a |
| b |
∴3
| a |
| b |
∵向量
| m |
| a |
| b |
∴4x=11y,①
∵|
| m |
| 137 |
∴x2+y2=4×137②
由①②解得
|
|
故向量
| m |
点评:本题考查了向量的坐标运算,以及向量的平行的条件,以及向量的模,属于基础题

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
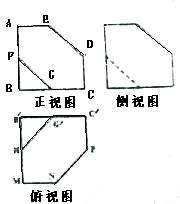 用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )
用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )| A、5 | ||
B、7-6
| ||
C、8-6
| ||
| D、4 |
“m>4”是“椭圆
+
=1(m>2)的焦距大于2”的( )
| x2 |
| m |
| y2 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若双曲线
-
=1(b>0)的一个顶点到与此顶点较远的一个焦点的距离为9,则双曲线的离心率是( )
| x2 |
| 16 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
