题目内容
若函数f（x）=
x3+x2-
在区间（a，a+5）内存在最小值，则实数a的取值范围是（ ）
| 1 |
| 3 |
| 2 |
| 3 |
| A、[-5，0） |
| B、（-5，0） |
| C、[-3，0） |
| D、（-3，0） |
考点：利用导数求闭区间上函数的最值
专题：计算题,作图题,导数的综合应用
分析：由题意，求导f′（x）=x2+2x=x（x+2）确定函数的单调性，从而作出函数的简图，由图象求实数a的取值范围．
解答：
解：由题意，f′（x）=x2+2x=x（x+2），
故f（x）在（-∞，-2），（0，+∞）上是增函数，
在（-2，0）上是减函数，
作其图象如右图，
令
x3+x2-
=-
得，
x=0或x=-3；
则结合图象可知，
；
解得，a∈[-3，0）；
故选C．
解：由题意，f′（x）=x2+2x=x（x+2），故f（x）在（-∞，-2），（0，+∞）上是增函数，
在（-2，0）上是减函数，
作其图象如右图，
令
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
x=0或x=-3；
则结合图象可知，
|
解得，a∈[-3，0）；
故选C．
点评：本题考查了导数的综合应用及学生作图识图的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
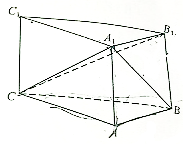如图，在三棱柱ABC-A1B1C1中，侧棱与底面垂直，∠CAB=90°，AC=2，BC=
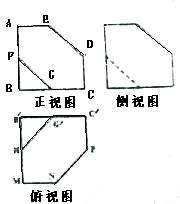用一平面截棱长为2的正方体，截得的多面体的三视图如图所示，ABCDE，B′MNPC′是边长为2的正方形的一角，其中AE=CD=MN=PC′=1，F，G，H，G′分别是所在各边的中点，其侧视图与正视图尺寸相同，则该多面体的体积是（ ）
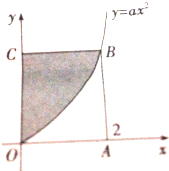如图，长方形的四个顶点为O（0，0），A（2，0），B（2，4），C（0，4）曲线y=ax2经过点B，现将一质点随机投入正方形OABC中，则质点落在图中阴影区域的概率是