题目内容
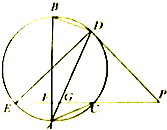 如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.(Ⅰ)求证:AB为圆的直径;
(Ⅱ)若AC=BD,AB=5,求弦DE的长.
考点:与圆有关的比例线段,直线和圆的方程的应用
专题:直线与圆
分析:(Ⅰ)由已知PG=PD,得到∠PDG=∠PGD,由切割弦定理得到∠PDA=∠DBA,进一步得到∠EGA=∠DBA,从而∠PFA=∠BDA.最后可得∠BDA=90°,说明AB为圆的直径;
(Ⅱ)连接BC,DC.由AB是直径得到∠BDA=∠ACB=90°,然后由Rt△BDA≌Rt△ACB,得到∠DAB=∠CBA.再由∠DCB=∠DAB可推得DC∥AB.进一步得到ED为直径,则ED长可求.
(Ⅱ)连接BC,DC.由AB是直径得到∠BDA=∠ACB=90°,然后由Rt△BDA≌Rt△ACB,得到∠DAB=∠CBA.再由∠DCB=∠DAB可推得DC∥AB.进一步得到ED为直径,则ED长可求.
解答:
(Ⅰ)证明:∵PG=PD,∴∠PDG=∠PGD,
由于PD为切线,故∠PDA=∠DBA,
又∵∠EGA=∠PGD,∴∠EGA=∠DBA,
∴∠DBA+∠BAD=∠EGA+∠BAD,
从而∠PFA=∠BDA.
又AF⊥EP,∴∠PFA=90°,则∠BDA=90°,
故AB为圆的直径.

(Ⅱ)解:连接BC,DC.
由于AB是直径,故∠BDA=∠ACB=90°.
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而得Rt△BDA≌Rt△ACB,
于是∠DAB=∠CBA.
又∵∠DCB=∠DAB,∴∠DCB=∠CBA,故DC∥AB.
∵AB⊥EP,∴DC⊥EP,∠DCE为直角,
∴ED为直径,又由(1)知AB为圆的直径,
∴DE=AB=5.
由于PD为切线,故∠PDA=∠DBA,
又∵∠EGA=∠PGD,∴∠EGA=∠DBA,
∴∠DBA+∠BAD=∠EGA+∠BAD,
从而∠PFA=∠BDA.
又AF⊥EP,∴∠PFA=90°,则∠BDA=90°,
故AB为圆的直径.

(Ⅱ)解:连接BC,DC.
由于AB是直径,故∠BDA=∠ACB=90°.
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而得Rt△BDA≌Rt△ACB,
于是∠DAB=∠CBA.
又∵∠DCB=∠DAB,∴∠DCB=∠CBA,故DC∥AB.
∵AB⊥EP,∴DC⊥EP,∠DCE为直角,
∴ED为直径,又由(1)知AB为圆的直径,
∴DE=AB=5.
点评:本题考查了直线和圆的位置关系,考查了圆的切割线定理的应用,是中档题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
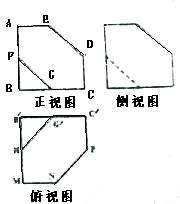 用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )
用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )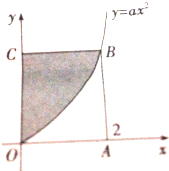 如图,长方形的四个顶点为O(0,0),A(2,0),B(2,4),C(0,4)曲线y=ax2经过点B,现将一质点随机投入正方形OABC中,则质点落在图中阴影区域的概率是
如图,长方形的四个顶点为O(0,0),A(2,0),B(2,4),C(0,4)曲线y=ax2经过点B,现将一质点随机投入正方形OABC中,则质点落在图中阴影区域的概率是