题目内容
某学校为了丰富学生的业余生活,以班级为单位组织学生开展古诗词背诵比赛,随机抽取题目,背诵正确加10分,背诵错误减10分,只有“正确”和“错误”两种结果,其中某班级的正确率为p=
,背诵错误的概率为q=
,现记“该班级完成n首背诵后总得分为Sn”.
(Ⅰ) 求S6=20且Si≥0(i=1,2,3)的概率;
(Ⅱ)记ξ=|S5|,求ξ的分布列及数学期望.
| 2 |
| 3 |
| 1 |
| 3 |
(Ⅰ) 求S6=20且Si≥0(i=1,2,3)的概率;
(Ⅱ)记ξ=|S5|,求ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式,离散型随机变量及其分布列
专题:计算题,概率与统计
分析:(Ⅰ)当S6=20时,即背诵6首后,正确个数为4首,错误2首,分类求概率求和;
(Ⅱ)∵ξ=|S5|的取值为10,30,50,又p=
,q=
,从而分别求概率以列出分布列,再求数学期望.
(Ⅱ)∵ξ=|S5|的取值为10,30,50,又p=
| 2 |
| 3 |
| 1 |
| 2 |
解答:
解:(Ⅰ)当S6=20时,即背诵6首后,正确个数为4首,错误2首,
若第一首和第二首背诵正确,则其余4首可任意背诵对2首;
若第一首正确,第二首背诵错误,第三首背诵正确,则其余3首可任意背诵对2首,
此时的概率为:p=(
)2×
×(
)2×(
)2+
×
×
×
×(
)2×
=
;
(Ⅱ)∵ξ=|S5|的取值为10,30,50,
又p=
,q=
,
∴P(ξ=10)=
(
)3(
)2+
(
)2(
)3=
,
P(ξ=30)=
(
)4(
)1+
(
)1(
)4=
,
P(ξ=50)=
(
)5+
(
)5=
.
∴ξ的分布列为:
∴Eξ=10×
+30×
+50×
=
.
若第一首和第二首背诵正确,则其余4首可任意背诵对2首;
若第一首正确,第二首背诵错误,第三首背诵正确,则其余3首可任意背诵对2首,
此时的概率为:p=(
| 2 |
| 3 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 16 |
| 81 |
(Ⅱ)∵ξ=|S5|的取值为10,30,50,
又p=
| 2 |
| 3 |
| 1 |
| 2 |
∴P(ξ=10)=
| C | 3 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 2 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 40 |
| 81 |
P(ξ=30)=
| C | 4 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 1 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 30 |
| 81 |
P(ξ=50)=
| C | 5 5 |
| 2 |
| 3 |
| C | 0 5 |
| 1 |
| 3 |
| 11 |
| 81 |
∴ξ的分布列为:
| ξ | 10 | 30 | 50 | ||||||||
|
|
|
|
| 40 |
| 81 |
| 30 |
| 81 |
| 11 |
| 81 |
| 1850 |
| 81 |
点评:本题考查了概率的求法及分布列的列法及数学期望的求法,属于基础题.

练习册系列答案
相关题目
 如图,圆O为等腰梯形ABCD的外接圆,且AB∥CD,过点C作圆的切线CE交AB的延长线于E,证明:
如图,圆O为等腰梯形ABCD的外接圆,且AB∥CD,过点C作圆的切线CE交AB的延长线于E,证明: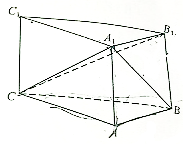 如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠CAB=90°,AC=2,BC=
如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠CAB=90°,AC=2,BC=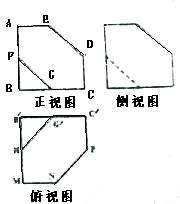 用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )
用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )