题目内容
“?x∈R,x2-ax+9>0”为真命题,则实数a的取值范围是 .
考点:命题的真假判断与应用
专题:简易逻辑
分析:本题的关键是“?x∈R,x2-ax+9>0”为真命题,结合二次函数的基本知识可以求出实数a的取值范围
解答:
解:∵“?x∈R,x2-ax+9>0”为真命题
∴△=a2-36<0
∴实数a的取值范围是:-6<a<6
故答案为:-6<a<6
∴△=a2-36<0
∴实数a的取值范围是:-6<a<6
故答案为:-6<a<6
点评:本题考查的是命题真假与参数范围问题,是高考中常见的题型

练习册系列答案
相关题目
执行如图所示的程序框图,则输出的a的值为( )(注:“a=2”,即为“a←2”或为“a:=2”.)
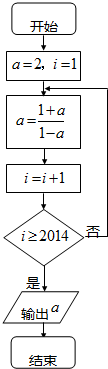

| A、2 | ||
B、
| ||
C、-
| ||
| D、-3 |
复数
的虚部为( )
| -2i |
| 1-i |
| A、i | B、-i | C、1 | D、-1 |
| ∫ |
-
|
| A、0 | B、π | C、2 | D、-2 |