题目内容
某公司以每吨10万元的价格销售某种化工产品,每年可售出1000吨,若将该产品每吨的价格上涨x%,则每年的销售量将减少mx%(m>0)
(1)当m=
时,求销售额的最大值;
(2)若涨价能使销售额增加,求m的取值范围.
(1)当m=
| 1 |
| 2 |
(2)若涨价能使销售额增加,求m的取值范围.
考点:函数最值的应用
专题:应用题,不等式的解法及应用
分析:(1)要求当m=
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大,我们要根据已知条件先构造出函数的解析式,然后根据二次函数求最值的方法,求出销售的总金额的最大值.
(2)由(1)中的解析式,我们易得-mx2+100(1-m)x+10000>10000,解不等式,即可求出m的取值范围.
| 1 |
| 2 |
(2)由(1)中的解析式,我们易得-mx2+100(1-m)x+10000>10000,解不等式,即可求出m的取值范围.
解答:
解:(1)设产品每吨价格上涨x%时,销售总金额为y元.
则y=10(1+x%)•1000(1-mx%)
=-mx2+100(1-m)x+10000
当m=
时,y=-
(x-50)2+11250,
故当x=50时,ymax=11250(元).
(2)y=-mx2+100(1-m)x+10000
y=-mx2+100(1-m)x+10000>10000,
∴0<x<
,
∴
>0,
∴0<m<1.
则y=10(1+x%)•1000(1-mx%)
=-mx2+100(1-m)x+10000
当m=
| 1 |
| 2 |
| 1 |
| 2 |
故当x=50时,ymax=11250(元).
(2)y=-mx2+100(1-m)x+10000
y=-mx2+100(1-m)x+10000>10000,
∴0<x<
| 100(1-m) |
| m |
∴
| 100(1-m) |
| m |
∴0<m<1.
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
相关题目
重庆实验外国语学校高二年级将从个班推选出来的6个男生,5个女生中任选3人组建“重外学生文明督察岗”,则下列事件中互斥不对立的事件是( )
| A、“3个都是男生”和“至多1个女生” |
| B、“至少有2个男生”和“至少两个女生” |
| C、“恰有2个女生”和“恰有1个或3个男生” |
| D、“至少有2个女生”和“恰有2个男生” |
已知集合M={x|-2<x<3},N={x|2x+1≥1},则M∩N等于( )
| A、(-2,-1] |
| B、(-2,1] |
| C、[1,3) |
| D、[-1,3) |
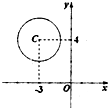 已知圆C:(x+3)2+(y-4)2=4
已知圆C:(x+3)2+(y-4)2=4