题目内容
已知数列{an}满足:a1=-4,an+1=2an-2n+1,若bn=
an,且存在n0,对于任意的k(k∈N*),不等式bn≤bn0成立,则n0的值为( )
n-10
| ||
| n+1 |
| A、11 | B、12 | C、13 | D、14 |
考点:数列递推式
专题:综合题,等差数列与等比数列
分析:先求出数列的通项,利用bn+1≥bn,确定n的范围,由此可得结论.
解答:
解:∵an+1=2an-2n+1,
∴
-
=-1,
∵a1=-4,∴
=-2,
∴{
}是以-2为首项,-1为公差的等差数列,
∴
=-2-(n-1)=-(n+1),
∴bn=
an=(10
-n)×2n,
令bn+1≥bn,则(10
-n-1)×2n+1≥(10
-n)×2n,∴n≤10
-2
∴当1≤n≤12时,bn+1>bn,当n≥时,bn+1<bn,
∴n0=13.
故选:C.
∴
| an+1 |
| 2n+1 |
| an |
| 2n |
∵a1=-4,∴
| a1 |
| 2 |
∴{
| an |
| 2n |
∴
| an |
| 2n |
∴bn=
n-10
| ||
| n+1 |
| 2 |
令bn+1≥bn,则(10
| 2 |
| 2 |
| 2 |
∴当1≤n≤12时,bn+1>bn,当n≥时,bn+1<bn,
∴n0=13.
故选:C.
点评:本题考查数列递推式,考查等差数列的证明.考查数列的通项,正确求通项是关键.

练习册系列答案
相关题目
已知函数f(x)=
,则f(f(-π))的值等于( )
|
|
| A、π2-1或0 |
| B、π2-1 |
| C、0 |
| D、-π |
如图所示,程序框图的输出结果为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
 读如图的程序:上面的程序如果在执行的时候,输入93,那么输出的结果为( )
读如图的程序:上面的程序如果在执行的时候,输入93,那么输出的结果为( )| A、99 | B、39 |
| C、39.3 | D、99.3 |
把89化这二进制数,其结果为( )
| A、1001101 |
| B、1100101 |
| C、1011011 |
| D、1011001 |
如果直线L过点P(3,-1),且与直线x+2y=0垂直,则直线L的方程为( )
| A、x-2y-5=0 |
| B、x+2y-5=0 |
| C、2x-y-7=0 |
| D、2x+y+7=0 |
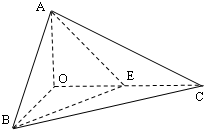 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.