题目内容

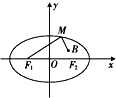如图，已知椭圆
x2
32
+
y2
16
=1内有一点B（2，2），F1、F2是其左、右焦点，M为椭圆上的动点，则|
MF1
|+|
MB
|的最小值为（　　）
A、4
2
B、6
2
C、4
D、6
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：借助于椭圆的定义把|
MF1
|+|
MB
|转化为2a-（|
MF2
|-|
MB
|），结合三角形中的两边之差小于第三边得答案．
解答： 解：|
MF1
|+|
MB
|=2a-（|
MF2
|-|
MB
|）≥2a-|
BF2
|=8
2
-2
2
=6
2
，
当且仅当M，F2，B共线时取得最小值6
2
．
故选：B．
点评：本题考查了与椭圆有关的最值得求法，考查了数学转化思想方法，是中档题．
练习册系列答案
相关题目
已知函数f（x）=ex-ax-1（a∈R）．
（1）试讨论函数f（x）的单调性；
（2）当a=1时，求证：当x≥0时f（x）≥f（-x）．
设Sn是正项数列{an}的前n项和，且Sn=
1
3
a
2
n
+
1
2
an．
（1）求an；
（2）设
bn
=
3
4an+3
（n∈N+），且数列{bn}的前n项和为Tn，试比较Tn与
1
4
的大小．
若抛物线的顶点是双曲线x2-y2=1的中心，焦点是双曲线的右顶点
（1）求抛物线的标准方程；
（2）若直线l过点C（2，1）交抛物线于M，N两点，是否存在直线l，使得C恰为弦MN的中点？若存在，求出直线l方程；若不存在，请说明理由．
若两个椭圆的离心率相同，则称此两个椭圆相似．已知椭圆的焦点在x轴上，与
x2
4
+
y2
3
=1相似且过点（2，3），则此椭圆的长轴长为（　　）
A、4B、6C、8D、16
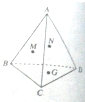如图，已知A为平面BCD外一点，M，N，G分别是△ABC、△ABD、△BCD的重心，求证：平面MNG∥平面ACD．
已知函数g（x）=|4x-x2|．
（1）作出函数的图象（直接作出图象即可）；
（2）若g（x）+a=0有三个根，求a的值．
某企业在第1年初购买一台价值为120万元的设备M，M的价值在使用过程中逐年减少，从第2年到第6年，每年初M的价值比上年初减少10万元；从第7年开始，每年初M的价值为上年初的75%．
（1）求第n年初M的价值an的表达式；
（2）设An=
a1+a2+…+an
n
若An大于80万元，则M继续使用，否则须在第n年初对M更新，证明：第6年初仍可对M继续使用．
已知f（x）是定义在R上的奇函数，f（-1）=0，若?x1，x2∈（-∞，0），且x1≠x2时
x1f(x1)-x2f(x2)
x1-x2
＜0恒成立，则不等式xf（x）＜0的解集为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网