题目内容
已知函数g(x)=|4x-x2|.
(1)作出函数的图象(直接作出图象即可);
(2)若g(x)+a=0有三个根,求a的值.
(1)作出函数的图象(直接作出图象即可);
(2)若g(x)+a=0有三个根,求a的值.
考点:函数的零点与方程根的关系,函数图象的作法
专题:函数的性质及应用
分析:(1)根据二次函数的图象和性质,结合函数图象的纵向对折变换,可得函数g(x)=|4x-x2|的图象;
(2)在直角坐标系中作出直线y=-a,由它与g(x)=|4x-x2|的交点情况即可求得a的值;
(2)在直角坐标系中作出直线y=-a,由它与g(x)=|4x-x2|的交点情况即可求得a的值;
解答:
解:(1)函数g(x)=|4x-x2|的图象如下图所示:

(2)在直角坐标系中作出直线y=-a,
由图可知:
当-a=4,即a=-4时,直线y=-a与g(x)=|4x-x2|的交点有三个,
即方程g(x)+a=0有三个根,
故a=-4.

(2)在直角坐标系中作出直线y=-a,
由图可知:
当-a=4,即a=-4时,直线y=-a与g(x)=|4x-x2|的交点有三个,
即方程g(x)+a=0有三个根,
故a=-4.
点评:本题考查二次函数的图象与性质,难点在于准确作图,着重考查数形结合思想与转化思想,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)作出函数f(x)的图象,并指出函数f(x)的单调区间;
(2)根据图象写出不等式f(x)>0的解集;
(3)求当x∈[1,5]时函数的值域.
(1)作出函数f(x)的图象,并指出函数f(x)的单调区间;
(2)根据图象写出不等式f(x)>0的解集;
(3)求当x∈[1,5]时函数的值域.
已知关于x的方程x2+kx-2=0的一个根是1,则它的另一个根是( )
| A、-3 | B、3 | C、-2 | D、2 |
动点P(cosθ,sinθ)(θ∈R)关于直线y=x-2的对称点是P′,则|PP′|的最大值( )
A、2
| ||
B、
| ||
C、2
| ||
D、2
|
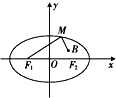 如图,已知椭圆
如图,已知椭圆