题目内容
已知函数f(x)=ex-ax-1(a∈R).
(1)试讨论函数f(x)的单调性;
(2)当a=1时,求证:当x≥0时f(x)≥f(-x).
(1)试讨论函数f(x)的单调性;
(2)当a=1时,求证:当x≥0时f(x)≥f(-x).
考点:利用导数研究函数的单调性,函数恒成立问题
专题:计算题,导数的综合应用
分析:(1)求导f′(x)=ex-a,讨论导数的正负从而得到函数f(x)的单调性;
(2)化简f(x)-f(-x)=ex+e-x-2x;由导数证明函数的单调性,从而证明当x≥0时f(x)≥f(-x).
(2)化简f(x)-f(-x)=ex+e-x-2x;由导数证明函数的单调性,从而证明当x≥0时f(x)≥f(-x).
解答:
解:(1)∵f(x)=ex-ax-1,
f′(x)=ex-a;
①当a≤0时,f′(x)>0,
故f(x)=ex-ax-1在R上是增函数,
②当0<a时,
当x<lna时,f′(x)<0,
当x>lna时,f′(x)>0,
故f(x)=ex-ax-1在(-∞,lna)上是减函数,
在(lna,+∞)上是增函数;
(2)证明:当a=1时,由(1)知,
f(x)=ex-x-1在(-∞,0)上是减函数,
在(0,+∞)上是增函数;
∵f(x)-f(-x)=ex+e-x-2x;
∴f′(x)-f′(-x)=ex-e-x-2,
∵x≥0,
∴f′(x)-f′(-x)≥0,
故f(x)-f(-x)≥f(0)-f(0)=0;
故f(x)≥f(-x).
f′(x)=ex-a;
①当a≤0时,f′(x)>0,
故f(x)=ex-ax-1在R上是增函数,
②当0<a时,
当x<lna时,f′(x)<0,
当x>lna时,f′(x)>0,
故f(x)=ex-ax-1在(-∞,lna)上是减函数,
在(lna,+∞)上是增函数;
(2)证明:当a=1时,由(1)知,
f(x)=ex-x-1在(-∞,0)上是减函数,
在(0,+∞)上是增函数;
∵f(x)-f(-x)=ex+e-x-2x;
∴f′(x)-f′(-x)=ex-e-x-2,
∵x≥0,
∴f′(x)-f′(-x)≥0,
故f(x)-f(-x)≥f(0)-f(0)=0;
故f(x)≥f(-x).
点评:本题考查导数的综合应用,属于中档题.

练习册系列答案
相关题目
已知AB是异面直线l1与l2的公垂线段,且AB=3,异面直线l1与l2所成的角为30°,在l1上取AP=6,则点P到l2的距离为( )
| A、6 | ||
B、3
| ||
C、6或3
| ||
D、2
|

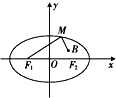 如图,已知椭圆
如图,已知椭圆