题目内容
已知f（x）是二次函数，关于x的方程mf2（x）+nf（x）+p=0（m，n，p为实数）有4个不同的实数根，且它们从小到大的顺序为：x1＜x2＜x3＜x4，则x1-x2-x3+x4的值为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：关于x的方程mf2（x）+nf（x）+p=0的解必是f（x）=k1与f（x）=k2的解，不妨设k1＞k2，则由题意f（x）=k1的解为x1，x4；f（x）=k2的解为x2，x3，则x1+x4=x2+x3，进而得到答案．
解答：
解：设关于k的方程mk2+nk+p=0的两个根为k1，k2，不妨设k1＞k2，
则关于x的方程mf2（x）+nf（x）+p=0的解必是f（x）=k1与f（x）=k2的解，
∵x1＜x2＜x3＜x4，
∴可令f（x）=k1的解为x1，x4；f（x）=k2的解为x2，x3，
由韦达定理可得：
x1+x4=x2+x3=-
（其中a，b分别为二次函数f（x）的二次项和一次项系数）
∴x1-x2-x3+x4=0，
故答案为：0
则关于x的方程mf2（x）+nf（x）+p=0的解必是f（x）=k1与f（x）=k2的解，
∵x1＜x2＜x3＜x4，
∴可令f（x）=k1的解为x1，x4；f（x）=k2的解为x2，x3，
由韦达定理可得：
x1+x4=x2+x3=-
| b |
| a |
∴x1-x2-x3+x4=0，
故答案为：0
点评：本题考查的知识点是方程的根，二次函数图象和性质，其中将关于x的方程mf2（x）+nf（x）+p=0的解转化f（x）=k1与f（x）=k2的解，是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
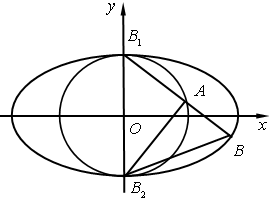已知椭圆C1：
如图，如果你在海边沿着海岸线直线前行，请设计一种测量海中两个小岛A，B之间距离的方法．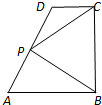
如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设