题目内容
一批货物随17列货车从A市以v千米/小时匀速直达B市,已知两地铁路线长为400千米,为了安全,两列货车的间距不得少于(
)2千米,那么这批货物全部运到B市最快需要( )
| v |
| 20 |
| A、6小时 | B、8小时 |
| C、10小时 | D、12小时 |
考点:函数模型的选择与应用
专题:应用题,不等式的解法及应用
分析:根据题意设出把货物全部运到B市的时间为y,表示出y的解析式,利用基本不等式求出y的最小值即可.
解答:
解:设这批物资全部运到B市用的时间为y小时
因为不计货车的身长,所以设列车为一个点,可知最前的点与最后的点之间距离最小值为16×(
)2千米时,时间最快.
则y=
=
+
≥2
,
当且仅当
=
即v=100千米/小时时,时间ymin=8小时.
故选:B.
因为不计货车的身长,所以设列车为一个点,可知最前的点与最后的点之间距离最小值为16×(
| v |
| 20 |
则y=
(
| ||
| v |
| v |
| 25 |
| 400 |
| v |
|
当且仅当
| v |
| 25 |
| 400 |
| v |
故选:B.
点评:本题主要考查了函数模型的选择与应用,以及利用基本不等式求最值,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
若复数z满足z•(1-i)=2-i(其中i是虚数单位),则z=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若直线y=|
|x+1与直线y=|
|x平行,
,
为非零向量,则必有( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、(
| ||||||||
D、(
|
将函数y=sin2x+
cos2x(x∈R)的图象向右平移m(m>0)个单位长度后,所得到的图象关于原点对称,则m的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p、q,则“p且q为假”是“p或q为真”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列说法正确的是( )
| A、“a>b”是“a2>b2”的充分不必要条件 |
| B、命题“?x0∈R,x02+1<0”的否定是:“?x∈R,x2+1>0” |
| C、关于x的方程x2+(a+1)x+a-2=0的两根异号的充要条件是a<1 |
| D、若f(x)为R上的偶函数,则f(x-1)的图象关于直线x=1对称 |
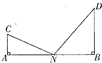 如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为
如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为 若如图框图所给程序运行的结果为S=360,那么判断框中应填入的关于k的判断条件是k<
若如图框图所给程序运行的结果为S=360,那么判断框中应填入的关于k的判断条件是k<