Question

1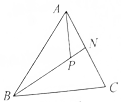．如图，在△ABC中，已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$，P是BN上一点，若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$，则实数m的值是$\frac{1}{2}$．

Answer 1

分析 由于B，P，N三点共线，利用向量共线定理可得：存在实数λ使得$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+（1-λ）$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+$\frac{1-λ}{2}$$\overrightarrow{AC}$，又$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$，利用共面向量基本定理即可得出．

解答 解：∵B，P，N三点共线，
∴存在实数λ使得$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+（1-λ）$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+$\frac{1-λ}{2}$$\overrightarrow{AC}$，
又$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$，
∴$\left\{\begin{array}{l}{m=λ}\\{\frac{1}{4}=\frac{1-λ}{2}}\end{array}\right.$，解得m=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评 本题考查了向量共线定理、共面向量基本定理，属于基础题．