题目内容
设二次函数f(x)=ax2+bx+c在区间[-2,2]上的最大值、最小值分别为M、m,集合A={x|f(x)-x=0}.
(1)若f(0)=2,且A={1,2},求a,b,c;
(2)在(1)的条件下,求M和m的值;
(3)若A={2},且a≥1,记g(a)=M-m,求g(a)的解析式.
(1)若f(0)=2,且A={1,2},求a,b,c;
(2)在(1)的条件下,求M和m的值;
(3)若A={2},且a≥1,记g(a)=M-m,求g(a)的解析式.
考点:二次函数的性质,函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:(1)由f(0)=2,求得c,再由A={1,2}得1,2是方程ax2+(b-1)x+c=0的两根,运用韦达定理,即可得到a,b;
(2)运用二次函数的对称轴和区间的关系,即可得到M,m;
(3)运用韦达定理,求得b,c都用a表示,再由二次函数的对称轴和区间的关系,即可得到g(a).
(2)运用二次函数的对称轴和区间的关系,即可得到M,m;
(3)运用韦达定理,求得b,c都用a表示,再由二次函数的对称轴和区间的关系,即可得到g(a).
解答:
解:(1)f(0)=c=2,
由 A={1,2}得1,2是方程ax2+(b-1)x+c=0的两根,
由韦达定理
得:a=1,b=-2,c=2.
(2)f(x)=x2-2x+2的对称轴为x=1,开口向上,
当x∈[-2,2]时,m=f(1)=1,M=f(-2)=10;
(3)由A={2},得ax2+(b-1)x+c=0有2个相等实根2,
∴
即
∴f(x)=ax2+(1-4a)x+4a,
其对称轴为x=-
=2-
开口向上,
∵a≥1∴0<
≤
∴
≤2-
<2
∴m=f(2-
)=2-
M=f(-2)=16a-2,
∴g(a)=M-m=16a+
-4.
由 A={1,2}得1,2是方程ax2+(b-1)x+c=0的两根,
由韦达定理
|
(2)f(x)=x2-2x+2的对称轴为x=1,开口向上,
当x∈[-2,2]时,m=f(1)=1,M=f(-2)=10;
(3)由A={2},得ax2+(b-1)x+c=0有2个相等实根2,
∴
|
|
其对称轴为x=-
| 1-4a |
| 2a |
| 1 |
| 2a |
∵a≥1∴0<
| 1 |
| 2a |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2a |
∴m=f(2-
| 1 |
| 2a |
| 1 |
| 4a |
∴g(a)=M-m=16a+
| 1 |
| 4a |
点评:本题考查二次函数在闭区间上的最值,考查二次方程的韦达定理及运用,考查运算能力,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
(x+1)5展开式的二项式系数的和是( )
| A、6 | B、128 | C、32 | D、64 |
一个正三棱柱的三视图如图所示,则这个正三棱柱的侧面积为( )
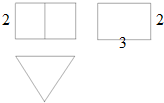

| A、18 | ||
B、6
| ||
C、12
| ||
D、18
|
下列函数中,既是偶函数又在区间(-∞,0)上单调递减的是( )
A、f(x)=
| ||
| B、f(x)=x2+1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
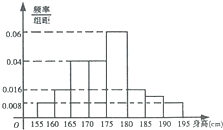 从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图:
从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图: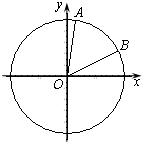 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别交单位圆于A、B两点.已知A、B两点的横坐标分别是
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别交单位圆于A、B两点.已知A、B两点的横坐标分别是