题目内容
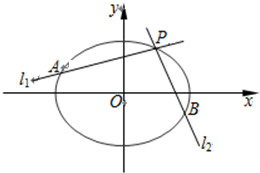
在直角坐标系xOy中 已知椭圆C：
+
=1上一点P（1，
），过点P的直线l1，l2与椭圆C分别交于点A、B，且他们的斜率k1，k2满足k1．k2=-
，求证：
（1）直线AB过定点；
（2）求△PAB面积的最大值．
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 4 |
（1）直线AB过定点；
（2）求△PAB面积的最大值．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）设直线l1的方程为y=k1(x-1)+
，联立
，得(3+4k12)x2+(12k1-8k12)x+4k12-12k1-3=0，由此利用已知条件能证明A，B关于原点O对称，即直线AB过定点O．
（2）设A（x0，y0），B（-x0，-y0），x0≠±1，直线AB的方程为y0x-x0y=0，AB=2
，点P到直线AB的距离为d=
，点P到直线AB的距离为d=
，由此能求出△PAB面积的最大值．
| 3 |
| 2 |
|
（2）设A（x0，y0），B（-x0，-y0），x0≠±1，直线AB的方程为y0x-x0y=0，AB=2
| x02+y02 |
|y0-
| ||
|
|y0-
| ||
|
解答：
（1）证明：设直线l1的方程为y=k1(x-1)+
，
联立
，得(3+4k12)x2+(12k1-8k12)x+4k12-12k1-3=0，
解得x=1或x=
，即A（
，
），
同理，B（
，
），
∵k1k2=-
，∴k2=-
，
∴
=
=
，
同理，得
=
．
∴A，B关于原点O对称，即直线AB过定点O．
（2）由（1）可设A（x0，y0），B（-x0，-y0），x0≠±1，
则直线AB的方程为y0x-x0y=0，
∴AB=2
，点P到直线AB的距离为d=
，
∴AB=2
，
点P到直线AB的距离为d=
，
∴S△PAB=
AB•d=
•2
•
=|y0-
x0|，
令t=y0-
x0，
则y0=
x0+t，
代入
+
=1，得x02+tx0+
-1=0，
令△=t2-4(
-1)≥0，解得|t|≤2
，
当且仅当
或
时，
|t|有最大值2
，∴△PAB面积的最大值为2
．
（1）证明：设直线l1的方程为y=k1(x-1)+| 3 |
| 2 |
联立
|
解得x=1或x=
| 4k12-12k1-3 |
| 3+4k12 |
| 4k12-12k1-3 |
| 3+4k12 |
| -12k12-12k1+9 |
| 2(3+4k12) |
同理，B（
| 4k22-12k2-3 |
| 3+4k22 |
| -12k22-12k2+9 |
| 2(3+4k22) |
∵k1k2=-
| 3 |
| 4 |
| 3 |
| 4k1 |
∴
| 4k22-12k2-3 |
| 3+4k22 |
4(-
| ||||
3+4(-
|
| -4k12+12k1+3 |
| 3+4k12 |
同理，得
| -12k22-12k2+9 |
| 2(3+4k22) |
| 12k12+12k1-9 |
| 2(3+4k12) |
∴A，B关于原点O对称，即直线AB过定点O．
（2）由（1）可设A（x0，y0），B（-x0，-y0），x0≠±1，
则直线AB的方程为y0x-x0y=0，
∴AB=2
| x02+y02 |
|y0-
| ||
|
∴AB=2
| x02+y02 |
点P到直线AB的距离为d=
|y0-
| ||
|
∴S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| x02+y02 |
|y0-
| ||
|
| 3 |
| 2 |
令t=y0-
| 3 |
| 2 |
则y0=
| 3 |
| 2 |
代入
| x02 |
| 4 |
| y02 |
| 3 |
| t2 |
| 3 |
令△=t2-4(
| t2 |
| 3 |
| 3 |
当且仅当
|
|
|t|有最大值2
| 3 |
| 3 |
点评：本题考查直线过定点的证明，考查三角形面积的最大值的求法，解题时要认真审题，注意点到直线的距离公式的合理运用．
练习册系列答案
优等生题库系列答案
相关题目
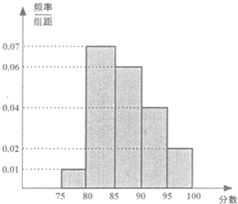一企业某次招聘新员工分笔试和面试两部分，人力资源部经理把参加笔试的40名学生的成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100），得到频率分布直方图如图所示．
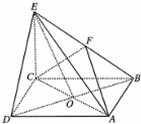在四棱锥E-ABCD中，底面ABCD是正方形，AC与BD交于点O，EC⊥底面ABCD，F为BE的中点．