题目内容
2.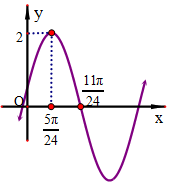 已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.
已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再利用正弦函数的单调性,求得函数的单调增区间.
解答 解:由题意,可得A=2,T=4($\frac{11π}{24}$-$\frac{5π}{24}$)=π,求得ω=2,
再根据五点法作图可得$\frac{5π}{24}$•2+φ=$\frac{π}{2}$,∴φ=$\frac{π}{12}$,
∴f(x)=2sin(2x+$\frac{π}{12}$).
y=f(x)+cos(ωx+$\frac{7π}{12}$)=2sin(2x+$\frac{π}{12}$)+cos(2x+$\frac{7π}{12}$)=sin(2x+$\frac{π}{12}$)
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{12}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{7}{24}$π≤x≤kπ+$\frac{5π}{24}$,
可得函数的增区间为[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z,
故答案为[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,正弦函数的单调性,属于基础题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
10.已知椭圆与双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$有共同的焦点,且离心率为$\frac{{\sqrt{5}}}{5}$,则椭圆的标准方程为( )
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |
17.下列函数中,在其定义域内是增函数而且又是奇函数的是( )
| A. | $y=x+\frac{1}{x}$ | B. | y=2x-2-x | C. | y=log2|x| | D. | y=2x+2-x |
7.已知$\frac{sinα-2cosα}{2sinα+3cosα}=2$,那么tanα的值为( )
| A. | -2 | B. | $-\frac{8}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
14.已知$sinα-2cosα=\frac{{\sqrt{10}}}{2}$,则tan2α=( )
| A. | $\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
12.“z1与z2互为共轭复数”是“z1z2∈R”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |