题目内容
已知函数 ,函数
,函数 ,函数
,函数
(1)当函数 在
在 时为减函数,求a的范围;
时为减函数,求a的范围;
(2)若a=e(e为自然对数的底数);
①求函数g(x)的单调区间;
②证明:
(1)因为函数 在
在 时为减函数,所以
时为减函数,所以 .
.
 .
.
因为 ,所以
,所以 ,
, 即
即 .
.
(i)当a=e时,
所以 =
=
记 ,则
,则 ,当
,当
当 所以
所以 >0.
>0.
所以在 ,在
,在 ;
;
即g(x)的单调増区间为 单调减区间为
单调减区间为
(ii)证明:由(i)得 欲证
欲证 ,
,
只需证
即证 .
.
记 ,则
,则
当 ,
, ,
,
当 ,
, 。即
。即
由(i)得 .所以
.所以 .
.

练习册系列答案
相关题目
 ,集合
,集合 ,
, ,则
,则 .
. 中,
中, 分别为
分别为 的中点,
的中点, ,点
,点 在线段
在线段 上,且
上,且 .
. ;
; 为线段
为线段 上一点,试确定
上一点,试确定 平面
平面 .
.
 如果目标函数z=x—y的最小值为-2,则实数m的值为______.
如果目标函数z=x—y的最小值为-2,则实数m的值为______. 并且m+3n=1则
并且m+3n=1则 的最小值__________ .
的最小值__________ . R,且|x+y|≤
R,且|x+y|≤ , |x-y|≤
, |x-y|≤ ,求证:|5x+y|≤1.
,求证:|5x+y|≤1. 的值为11,则输入自然数
的值为11,则输入自然数 的值是 .
的值是 .
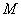 有特征值
有特征值 ,及对应的一个特征向量
,及对应的一个特征向量 ,并且
,并且 .变换成
.变换成 ,求矩阵
,求矩阵 与直线
与直线 交于
交于 两点,点
两点,点 在直线
在直线 上,且
上,且 ,则
,则 的取值范围为 .
的取值范围为 .