题目内容
8. 如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.(I)证明:平面POC⊥平面PAD;
(II)若CD=$\sqrt{2}$,三棱锥P-ABD与C-PBD的体积分别为V1、V2,求证V1=2V2.
分析 (Ⅰ)推导出OC⊥AD,OC⊥PO,OC⊥平面PAD,由此能证明平面POC⊥平面PAD.
(Ⅱ)推导出OC⊥OD,AD=2,设点P到平面ABCD的距离为h,由平行线BC与AD之间的距离为1,能证明V1=2V2.
解答 证明:(Ⅰ)在四边形OABC中,
∵AO∥BC,AO=BC,AB⊥AD,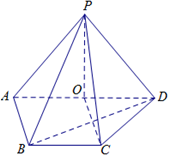
∴四边形OABC是正方形,得OC⊥AD,(2分)
在△POC中,∵PO2+OC2=PC2,∴OC⊥PO,(4分)
又PO∩AD=O,∴OC⊥平面PAD,
又OC?平面POC,
∴平面POC⊥平面PAD.(6分)
(Ⅱ)由(Ⅰ)知,四边形ABCO为正方形,
∴OC=AB=1,OC⊥OD,(8分)
∴$OD=\sqrt{C{D^2}-O{C^2}}=1$,从而AD=2,(9分)
设点P到平面ABCD的距离为h,∵平行线BC与AD之间的距离为1,
∴$\frac{V_1}{V_2}=\frac{{\frac{1}{3}{S_{△ABD}}•h}}{{\frac{1}{3}{S_{△BCD}}•h}}=\frac{{{S_{△ABD}}}}{{{S_{△BCD}}}}=\frac{{\frac{1}{2}AD•1}}{{\frac{1}{2}BC•1}}=\frac{AD}{BC}=2$,(11分)
即V1=2V2.(12分)
点评 本题考查面面垂直的证明,考查两几何体体积的数量关系的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
18.两座灯塔A和B与海洋观测站C的距离分别是akm和2akm,灯塔A在观测站C的北偏东20°,灯塔B在观测站C的南偏东70°,则灯塔A与灯塔B之间的距离为( )
| A. | $\sqrt{3}$akm | B. | 2akm | C. | $\sqrt{5}$akm | D. | $\sqrt{7}$akm |
19.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则双曲线的离心率的取值范围是( )
| A. | (1,+∞) | B. | $(1,1+\sqrt{2})$ | C. | $(1,\sqrt{3})$ | D. | $(1-\sqrt{2},1+\sqrt{2})$ |
16.若变量x,y满足条件$\left\{\begin{array}{l}3x-y≤0\\ x-3y+5≥0\\ x≥0\end{array}\right.$则z=x+y的最大值为( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{5}{3}$ | D. | 0 |