已知幂函数y=f(x)的图象过点($\sqrt{3}$.$\frac{1}{3}$).则f=4．题目和参考答案——青夏教育精英家教网—

题目内容

20．已知幂函数y=f（x）的图象过点（$\sqrt{3}$，$\frac{1}{3}$），则f（$\frac{1}{2}$）=4．

分析在解答时可以先设出幂函数的解析式，由于过定点，从而可解得函数的解析式，故而获得问题的解答．

解答解：∵幂函数y=f（x）=x^α的图象过点（$\sqrt{3}$，$\frac{1}{3}$），
∴${\sqrt{3}}^{α}$=$\frac{1}{3}$，解得：α=-2，
故f（x）=x^-2，f（$\frac{1}{2}$）=${（\frac{1}{2}）}^{-2}$=4，
故答案为：4．

点评本题考查的是幂函数的图象与性质以及求解析式问题．在解答的过程当中充分体现了幂函数的定义、性质知识的应用，同时待定系数法求参数的思想在此题中也得到了淋漓尽致的展现．

练习册系列答案

11．

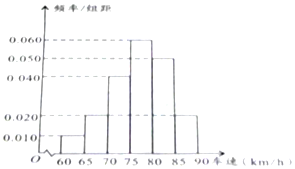“双节”期间，高速公路车辆较多，某调查公司在一服务区从七座以下的小型汽车中按进服务区的先后每间隔50辆就抽取一辆的样本方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段；[60，65），[65，70），[70，75），[75，80），[80，85），[85，90]后得到如图所示的频率分布直方图．
（1）求这40辆小型汽车车速的众数和中位数的估计值；
（2）若从车速在[60，70）内的车辆中任抽取2辆，求车速在[65，70）内的车辆恰有一辆的概率．

8．

如图，在四棱锥P-ABCD中，O∈AD，AD∥BC，AB⊥AD，AO=AB=BC=1，PO=$\sqrt{2}$，$PC=\sqrt{3}$．
（I）证明：平面POC⊥平面PAD；
（II）若CD=$\sqrt{2}$，三棱锥P-ABD与C-PBD的体积分别为V₁、V₂，求证V₁=2V₂．

15．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x（x＞0）}\\{{3}^{x}（x≤0）}\end{array}\right.$，且函数F（x）=f（x）+x-a有且仅有两个零点，则实数a的取值范围是a≤1．

5．若函数f（x）=x²-ax+2a-4的一个零点在区间（-2，0）内，另一个零点在区间（1，3）内，则实数a的取值范围是（0，2）．

12．已知函数f（x）=（$\frac{1}{2}$）^x-2^x．
（1）若f（x）=$\frac{15}{4}$，求x的值；
（2）若不等式f（2m-mcosθ）+f（-1-cosθ）＜f（0）对所有θ∈[0，$\frac{π}{2}$]都成立，求实数m的取值范围．

9．设直线l₁：mx-2my-6=0与l₂：（3-m）x+my+m²-3m=0．
（1）若l₁∥l₂，求l₁，l₂之间的距离；
（2）若直线l₂与两坐标轴的正半轴围成的三角形的面积最大，求直线l₂的方程．

10．抛物线$y=-\frac{1}{4}{x^2}$的准线方程是（　　）

试题分类