题目内容
19.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则双曲线的离心率的取值范围是( )| A. | (1,+∞) | B. | $(1,1+\sqrt{2})$ | C. | $(1,\sqrt{3})$ | D. | $(1-\sqrt{2},1+\sqrt{2})$ |
分析 由过F1且垂直于x轴的直线与双曲线交于A、B两点可知△ABC为锐角三角形,△ABF2为锐角三角形只要∠AF2B为锐角即可,由此可知$\frac{{b}^{2}}{a}$<2c,从而能够推导出该双曲线的离心率e的取值范围.
解答 解:由题设条件可知△ABF2为等腰三角形,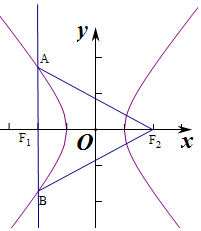
若△ABF2是锐角三角形,
只要∠AF2B为锐角,
即∠AF2B<45°,
即AF1<F1F2即可;
当x=-c时,$\frac{{c}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,得y=±$\frac{{b}^{2}}{a}$,
设A(-c,$\frac{{b}^{2}}{a}$),
∴$\frac{{b}^{2}}{a}$<2c,
即2ac>c2-a2,
得e2-2e-1<0
解出e∈(1,1+$\sqrt{2}$),
故选:B.
点评 本题考查双曲线的标准方程,以及双曲线的简单性质的应用.根据条件得到∠AF2B<45°是解决本题的关键.

练习册系列答案
相关题目
7.在平面内,一只蚂蚁从点A(-2,-3)出发,爬到y轴后又爬到圆(x+3)2+(y-2)2=2上,则它爬到的最短路程是( )
| A. | 5$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{26}$ | D. | $\sqrt{26}$-$\sqrt{2}$ |
14.调查某高中1000名学生的肥胖情况,得如表:
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15
(Ⅰ)求x的值
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取100名,问应在肥胖学生中抽多少名?
(Ⅲ)已知y≥194,z≥193,求肥胖学生中男生不少于女生的概率.
| 偏瘦 | 正常 | 肥胖 | |
| 女生(人) | 100 | 163 | y |
| 男生(人) | x | 187 | z |
(Ⅰ)求x的值
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取100名,问应在肥胖学生中抽多少名?
(Ⅲ)已知y≥194,z≥193,求肥胖学生中男生不少于女生的概率.
4.直线x-2017=0的倾斜角为( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | 不存在 |
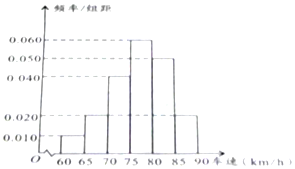 “双节”期间,高速公路车辆较多,某调查公司在一服务区从七座以下的小型汽车中按进服务区的先后每间隔50辆就抽取一辆的样本方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段;[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.
“双节”期间,高速公路车辆较多,某调查公司在一服务区从七座以下的小型汽车中按进服务区的先后每间隔50辆就抽取一辆的样本方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段;[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图. 如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.