题目内容
抛物线C:y2=2px经过点M(4,-4),
(1)不过点M的直线l分别交抛物线于A、B两点,当直线l的斜率为
,求证:直线MA与直线MB的倾斜角互补.
(2)不经过点M的动直线l交抛物线C于P、Q两点,且以PQ为直径的圆过点M,那么直线l是否过定点?如果是,求定点的坐标;如果不是,说明理由.
(1)不过点M的直线l分别交抛物线于A、B两点,当直线l的斜率为
| 1 |
| 2 |
(2)不经过点M的动直线l交抛物线C于P、Q两点,且以PQ为直径的圆过点M,那么直线l是否过定点?如果是,求定点的坐标;如果不是,说明理由.
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)代入点M,即可得到抛物线方程,设A(x1,y1),B(x2,y2),设直线l的方程是y=
x+m,联立抛物线方程,消去x,得到y的二次方程,运用韦达定理,以及直线的斜率公式,化简整理即可得证;
(2)设P(x1,y1),Q(x2,y2),以PQ为直径的圆过点M,则由
⊥
,即有
•
=0,由数量积的坐标公式,结合抛物线方程,即可得y1y2-4(y1+y2)=32=0,再由直线方程,即可得到定点.
| 1 |
| 2 |
(2)设P(x1,y1),Q(x2,y2),以PQ为直径的圆过点M,则由
| MP |
| MQ |
| MP |
| MQ |
解答:
(1)证明:抛物线C:y2=2px经过点M(4,-4),
即有16=8p,解得,p=2.
则抛物线方程为y2=4x,
设A(x1,y1),B(x2,y2),设直线l的方程是y=
x+m,
由
,得y2-8y+8m=0,
kAM+kBM=
+
=
+
=
=0,
则直线MA与直线MB的倾斜角互补.
(2)解:设P(x1,y1),Q(x2,y2),以PQ为直径的圆过点M,则由
⊥
,
即有
•
=0,
则(x1-4)(x2-4)+(y1+4)(y2+4)=0,
即(
-4)(
-4)+(y1+4)(y2+4)=0,
化简,得y1y2-4(y1+y2)+32=0,
则过PQ的直线为y=
(x+
)=
(x+
)=
(x-8)+4,
则直线恒过定点(8,4).
即有16=8p,解得,p=2.
则抛物线方程为y2=4x,
设A(x1,y1),B(x2,y2),设直线l的方程是y=
| 1 |
| 2 |
由
|
|
| y1+4 |
| x1-4 |
| y2+4 |
| x2-4 |
| 4 |
| y1-4 |
| 4 |
| y2-4 |
| 4(y1+y2-8) |
| (y1-4)(y2-4) |
则直线MA与直线MB的倾斜角互补.
(2)解:设P(x1,y1),Q(x2,y2),以PQ为直径的圆过点M,则由
| MP |
| MQ |
即有
| MP |
| MQ |
则(x1-4)(x2-4)+(y1+4)(y2+4)=0,
即(
| ||
| 4 |
| ||
| 4 |
化简,得y1y2-4(y1+y2)+32=0,
则过PQ的直线为y=
| 4 |
| y1+y2 |
| y1y2 |
| 4 |
| 4 |
| y1+y2 |
| 4(y1+y2)-32 |
| 4 |
| 4 |
| y1+y2 |
则直线恒过定点(8,4).
点评:本题考查抛物线方程和运用,考查联立直线方程和抛物线方程,消去未知数,运用韦达定理,考查直线和圆的方程,以及直线的斜率公式的运用,考查运算能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
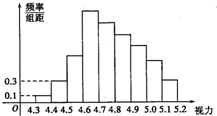 为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,视力在4.6到5.0之间的学生数为a,则a的值为( )
为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,视力在4.6到5.0之间的学生数为a,则a的值为( )| A、136 | B、146 |
| C、156 | D、166 |
 如图为函数f(x)=
如图为函数f(x)=| 2x |
| x2+1 |
| A、π | B、2π | C、3π | D、4π |