题目内容
16.已知1+i=$\frac{i}{z}$,则在复平面内,复数z所对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出.
解答 解:1+i=$\frac{i}{z}$,∴z=$\frac{i}{1+i}$=$\frac{i(1-i)}{(1+i)(1-i)}$=$\frac{1}{2}+\frac{1}{2}$i.
在复平面内,复数z所对应的点$(\frac{1}{2},\frac{1}{2})$在第一象限.
故选:A.
点评 本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
19.已知i为虚数单位,则复数z=(1+i)i对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.已知平面下列$\overrightarrow{a}$=(-2,3),$\overrightarrow{b}$=(1,2),向量λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$垂直,则实数λ的值为( )
| A. | $\frac{4}{13}$ | B. | -$\frac{4}{13}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
8.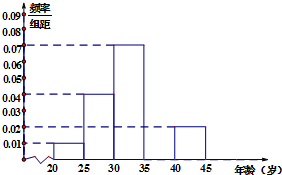 当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:
当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:
(1)求出表中的a,b,n的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在[30,40)的选取2名担任主要发言人.记这2名主要发言人年龄在[35,40)的人数为ξ,求ξ的分布列及数学期望.
 当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:
当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:| 组数 | 分组(单位:岁) | 频数 | 频率 |
| 1 | [20,25) | 5 | 0.05 |
| 2 | [25,30) | 20 | 0.20 |
| 3 | [30,35) | a | 0.35 |
| 4 | [35,40) | 30 | b |
| 5 | [40,45] | 10 | 0.10 |
| 合计 | n | 1.00 | |
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在[30,40)的选取2名担任主要发言人.记这2名主要发言人年龄在[35,40)的人数为ξ,求ξ的分布列及数学期望.
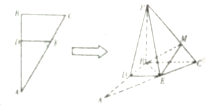 如图,在△ABC中,AB⊥BC,点D,E分别在AB,AC上,AD=2DB,AC=3EC,沿DE将△ADE翻折起来,使得点A到P的位置,满足$PB=\sqrt{3}BD$.
如图,在△ABC中,AB⊥BC,点D,E分别在AB,AC上,AD=2DB,AC=3EC,沿DE将△ADE翻折起来,使得点A到P的位置,满足$PB=\sqrt{3}BD$.