题目内容
1.已知平面下列$\overrightarrow{a}$=(-2,3),$\overrightarrow{b}$=(1,2),向量λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$垂直,则实数λ的值为( )| A. | $\frac{4}{13}$ | B. | -$\frac{4}{13}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
分析 依题意,可知(λ$\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=0,即(-2λ+1,3λ+2)•(1,2)=0,解之即可求得实数λ的值.
解答 解:∵$\overrightarrow{a}$=(-2,3),$\overrightarrow{b}$=(1,2),向量λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$垂直,
∴(-2λ+1,3λ+2)•(1,2)=-2λ+1+2(3λ+2)=4λ+5=0,
解得:λ=-$\frac{5}{4}$.
故选:D.
点评 本题考查平面向量数量积的运算,突出考查平面向量数量积的坐标运算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知集合A={x|x2-4<0},则∁RA=( )
| A. | {x|x≤-2或x≥2} | B. | {x|x<-2或x>2} | C. | {x|-2<x<2} | D. | {x|-2≤x≤2} |
5.已知流程图如图所示,该程序运行后,为使输出的f(x)值为16,则循环体的判断框内①处应( )
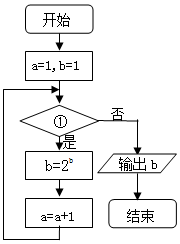

| A. | a>3? | B. | a≥3? | C. | a≤3? | D. | a<3? |
16.已知1+i=$\frac{i}{z}$,则在复平面内,复数z所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |