题目内容
已知F1,F2是双曲线
-
=1(a>0,b>0)的两个焦点,点P是该双曲线和圆x2+y2=a2+b2的一个交点,且△F1PF2的三边成等差数列,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,等差数列与等比数列,直线与圆,圆锥曲线的定义、性质与方程
分析:设P为双曲线右支上一点,PF1=m,PF2=n,由圆的方程可得F1,F2为圆直径的两个端点,运用勾股定理和双曲线的定义,以及等差数列的性质,化简整理计算,再由离心率公式即可得到.
解答:
解:设P为双曲线右支上一点,
PF1=m,PF2=n,
由于x2+y2=a2+b2=c2,
则F1,F2为圆直径的两个端点,
即有PF1⊥PF2,
即m2+n2=4c2,①
由双曲线的定义可得m-n=2a,②
又n,m,2c成等差数列,
则2c+n=2m,③
由①③可得,n=
c,m=
c,
代入②得
c=2a,
则e=
=5.
故答案为:5.
PF1=m,PF2=n,
由于x2+y2=a2+b2=c2,
则F1,F2为圆直径的两个端点,
即有PF1⊥PF2,
即m2+n2=4c2,①
由双曲线的定义可得m-n=2a,②
又n,m,2c成等差数列,
则2c+n=2m,③
由①③可得,n=
| 6 |
| 5 |
| 8 |
| 5 |
代入②得
| 2 |
| 5 |
则e=
| c |
| a |
故答案为:5.
点评:本题考查双曲线的定义和性质,考查离心率的求法,考查圆的直径所对的圆周角为直角,考查勾股定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知平面向量
与
的夹角为
,且|
|=1,|
+2
|=2
,则|
|=( )
| a |
| b |
| π |
| 3 |
| b |
| a |
| b |
| 3 |
| a |
| A、1 | ||
B、
| ||
| C、3 | ||
| D、2 |
已知x,y满足
,则
的最大值为( )
|
| 2y+x |
| x |
| A、5 | B、3 | C、2 | D、6 |
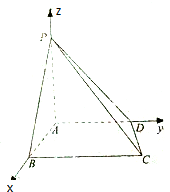 如图所示,四棱锥P-ABCD的顶点B、D、P分别在空间直角坐标系的坐标轴上,顶点A与原点重合;底面ABCD中,AB⊥BC,且BC=PA=3,AD=y;三棱锥P-ABC的体积为5.
如图所示,四棱锥P-ABCD的顶点B、D、P分别在空间直角坐标系的坐标轴上,顶点A与原点重合;底面ABCD中,AB⊥BC,且BC=PA=3,AD=y;三棱锥P-ABC的体积为5. 一个几何体的三视图如图所示,其中主视图、俯视图与左视图均是半径为2的圆,则这个几何体的表面积是
一个几何体的三视图如图所示,其中主视图、俯视图与左视图均是半径为2的圆,则这个几何体的表面积是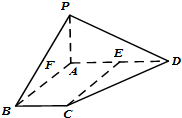 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=


