题目内容
若变量x,y满足约束条件
且z=3x+y的最小值为-8,则k=( )
|
| A、2 | B、-2 | C、3 | D、-3 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数z=3x+y的最小值为-8,建立条件关系即可求出k的值.
解答:
解:目标函数z=3x+y的最小值为-8,
∴y=-3x+z,要使目标函数z=3x+y的最小值为-1,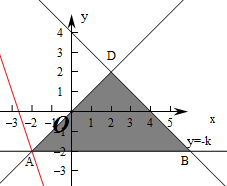
则平面区域位于直线y=-3x+z的右上方,即3x+y=-8,
作出不等式组对应的平面区域如图:
则目标函数经过点A时,目标函数z=3x+y的最小值为-8,
由
,解得
,
即A(-2,2),同时A也在直线x+k=0时,
即-2+k=0,
解得k=2,
故选:A
∴y=-3x+z,要使目标函数z=3x+y的最小值为-1,

则平面区域位于直线y=-3x+z的右上方,即3x+y=-8,
作出不等式组对应的平面区域如图:
则目标函数经过点A时,目标函数z=3x+y的最小值为-8,
由
|
|
即A(-2,2),同时A也在直线x+k=0时,
即-2+k=0,
解得k=2,
故选:A
点评:本题主要考查线性规划的应用,根据目标函数z=3x+y的最小值为-8,确定平面区域的位置,利用数形结合是解决本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若命题“?x∈R,x2+(a-1)x+1<0”是假命题,则实数a的取值范围是( )
| A、(1,4) |
| B、[-1,3] |
| C、[1,4] |
| D、(-∞,1]∪[3,+∞) |
对于定义域为R的函数f(x),若f(x)在(-∞,0)和(0,+∞)上均有零点,则称函数f(x)为“含界点函数”,则下列四个函数中,不是“含界点函数”的是( )
| A、f(x)=x2+bx-1(b∈R) |
| B、f(x)=2-|x-1| |
| C、f(x)=2x-x2 |
| D、f(x)=x-sinx |
函数f(x)=lgx-
的零点所在的区间为( )
| 1 |
| x |
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
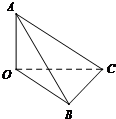 在三棱锥O-ABC中,已知OA,OB,OC两两垂直.OA=2,OB=
在三棱锥O-ABC中,已知OA,OB,OC两两垂直.OA=2,OB=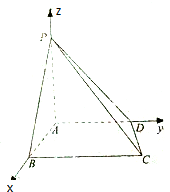 如图所示,四棱锥P-ABCD的顶点B、D、P分别在空间直角坐标系的坐标轴上,顶点A与原点重合;底面ABCD中,AB⊥BC,且BC=PA=3,AD=y;三棱锥P-ABC的体积为5.
如图所示,四棱锥P-ABCD的顶点B、D、P分别在空间直角坐标系的坐标轴上,顶点A与原点重合;底面ABCD中,AB⊥BC,且BC=PA=3,AD=y;三棱锥P-ABC的体积为5.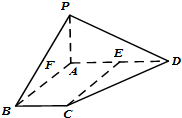 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=