题目内容
已知椭圆C:
+
=1(a>b>0)的右焦点为(
,0),离心率为
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于A,B两点,且以AB为直径的圆经过原点O,求证:点O到直线AB的距离为定值;
(Ⅲ)在(Ⅱ)的条件下,求△OAB面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于A,B两点,且以AB为直径的圆经过原点O,求证:点O到直线AB的距离为定值;
(Ⅲ)在(Ⅱ)的条件下,求△OAB面积的最大值.
考点:椭圆的应用
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据椭圆的右焦点为(
,0),离心率为
,求出c,a,可求b,即可求出椭圆C的方程;
(Ⅱ)分类讨论,设出直线AB的方程为y=kx+m,代入椭圆方程,利用韦达定理,结合以AB为直径的圆D经过坐标原点,根据点到直线的距离公式,即可得证;
(Ⅲ)分类讨论,求出|AB|的最大值,即可求△OAB面积的最大值.
| 2 |
| ||
| 3 |
(Ⅱ)分类讨论,设出直线AB的方程为y=kx+m,代入椭圆方程,利用韦达定理,结合以AB为直径的圆D经过坐标原点,根据点到直线的距离公式,即可得证;
(Ⅲ)分类讨论,求出|AB|的最大值,即可求△OAB面积的最大值.
解答:
(Ⅰ)解:∵椭圆的右焦点为(
,0),离心率为
,
∴
,
∴a=
,b=1,
∴椭圆C的方程为
+y2=1;
(Ⅱ)证明:直线AB斜率存在时,设直线AB的方程为y=kx+m,代入椭圆方程,
消元可得(1+3k2)x2+6kmx+3m2-3=0
∴x1+x2=-
,x1x2=
∵以AB为直径的圆D经过坐标原点,∴
•
=0
∴x1x2+y1y2=0,∴(1+k2)
-km×
+m2=0
∴4m2=3(k2+1)
∴原点O到直线的距离为d=
=
当直线AB斜率不存在时,由椭圆的对称性可知x1=x2,y1=-y2,
∵以AB为直径的圆D经过坐标原点,∴
•
=0
∴x1x2+y1y2=0,∴x12-y12=0
∵x12+3y12=3,∴|x1|=|y1|=
∴原点O到直线的距离为d=|x1|=
综上,点O到直线AB的距离为定值;
(Ⅲ)解:直线AB斜率存在时,由弦长公式可得|AB|=
|x1-x2|=
=
≤
=2,
当且仅当k=±
时,等号成立,
∴|AB|≤2,
直线AB斜率不存在时,|AB|=|y1-y2|=
<2,
∴△OAB面积=
|AB|d≤
×2×
=
,
∴△OAB面积的最大值为
.
| 2 |
| ||
| 3 |
∴
|
∴a=
| 3 |
∴椭圆C的方程为
| x2 |
| 3 |
(Ⅱ)证明:直线AB斜率存在时,设直线AB的方程为y=kx+m,代入椭圆方程,
消元可得(1+3k2)x2+6kmx+3m2-3=0
∴x1+x2=-
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
∵以AB为直径的圆D经过坐标原点,∴
| OA |
| OB |
∴x1x2+y1y2=0,∴(1+k2)
| 3m2-3 |
| 1+3k2 |
| 6km |
| 1+3k2 |
∴4m2=3(k2+1)
∴原点O到直线的距离为d=
| |m| | ||
|
| ||
| 2 |
当直线AB斜率不存在时,由椭圆的对称性可知x1=x2,y1=-y2,
∵以AB为直径的圆D经过坐标原点,∴
| OA |
| OB |
∴x1x2+y1y2=0,∴x12-y12=0
∵x12+3y12=3,∴|x1|=|y1|=
| ||
| 2 |
∴原点O到直线的距离为d=|x1|=
| ||
| 2 |
综上,点O到直线AB的距离为定值;
(Ⅲ)解:直线AB斜率存在时,由弦长公式可得|AB|=
| 1+k2 |
|
=
3+
|
3+
|
当且仅当k=±
| ||
| 3 |
∴|AB|≤2,
直线AB斜率不存在时,|AB|=|y1-y2|=
| 3 |
∴△OAB面积=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴△OAB面积的最大值为
| ||
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
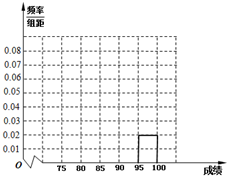 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.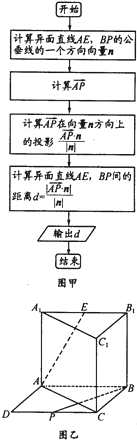 在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体
在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体