题目内容
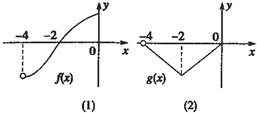 已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),它们在(-4,0]上的图象分别是图①和图②,则关于x的不等式f(x)•g(x)<0的解集是( )
已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),它们在(-4,0]上的图象分别是图①和图②,则关于x的不等式f(x)•g(x)<0的解集是( )| A、(-2,0)∪(2,4) |
| B、[0,4] |
| C、(2,4) |
| D、(-2,0] |
考点:函数的图象
专题:函数的性质及应用
分析:观察图象选择函数值同号的部分,再由f(x)是偶函数,g(x)是奇函数,得到f(x)•g(x)是奇函数,从而求得对称区间上的部分,最后两部分取并集.
解答:
解:如图所示:当x<0时
其解集为:(-2,0)
∵y=f(x)是偶函数,y=g(x)是奇函数
∴f(x)g(x)是奇函数
∴当x>0时,f(x)g(x)<0
∴其解集为:(2,4)
综上:不等式 f(x)•g(x)>0的解集是 (-2,0)∪(2,4)
故选A.
其解集为:(-2,0)
∵y=f(x)是偶函数,y=g(x)是奇函数
∴f(x)g(x)是奇函数
∴当x>0时,f(x)g(x)<0
∴其解集为:(2,4)
综上:不等式 f(x)•g(x)>0的解集是 (-2,0)∪(2,4)
故选A.
点评:本题主要考查函数的奇偶性在解不等式中的应用,还考查了数形结合,转化,分类讨论等思想方法.

练习册系列答案
相关题目
已知半径是13的球面上有A、B、C三点,AB=6,BC=8,AC=10,则球心到截面ABC的距离为( )
| A、12 | B、8 | C、6 | D、5 |
偶函数f(x)在区间[-8,-3]上单调递减,则函数f(x)在区间[3,8]上( )
| A、单调递增,且有最小值f(3) |
| B、单调递增,且有最大值f(3) |
| C、单调递减,且有最小值f(8) |
| D、单调递减,且有最大值f(8) |
已知函数f(x)=x2+(m-2)x+m2+12为偶函数,则m的值是( )
| A、1 | B、2 | C、3 | D、4 |