题目内容
已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1),且函数f(x)只有一个零点-1.
(1)求f(x)表达式;
(2)当x∈[-2,k]时,求函数f(x)的最小值;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=5x+m的图象上方,试确定实数m的取值范围.
(1)求f(x)表达式;
(2)当x∈[-2,k]时,求函数f(x)的最小值;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=5x+m的图象上方,试确定实数m的取值范围.
考点:函数恒成立问题,函数解析式的求解及常用方法,二次函数在闭区间上的最值
专题:压轴题,函数的性质及应用,不等式的解法及应用
分析:(1)由已知列关于a,b,c的方程组,求解方程组得到a,b,c的值,则函数解析式可求;
(2)分k在二次函数对称轴的两侧求得函数f(x)的最小值;
(3)构造函数令g(x)=f(x)-5x-m=x2-3x+1-m,x∈[-1,1],利用导数求其最小值,由最小值大于0求得m的取值范围.
(2)分k在二次函数对称轴的两侧求得函数f(x)的最小值;
(3)构造函数令g(x)=f(x)-5x-m=x2-3x+1-m,x∈[-1,1],利用导数求其最小值,由最小值大于0求得m的取值范围.
解答:
解:(1)由二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1),且函数f(x)只有一个零点-1,得
,解得a=1,b=2,c=1.
∴f(x)=(x+1)2;
(2)当x∈[-2,k]时,若-2≤k<-1,f(x)min=(k+1)2;
当x≥-1时,f(x)min=0.
∴f(x)min=
;
(3)令g(x)=f(x)-5x-m=x2-3x+1-m,x∈[-1,1],
则g′(x)=2x-3,
当x∈[-1,1]时g′(x)≤0恒成立,
∴g(x)在[-1,1]上为减函数,
g(x)min=1-3+1-m=-1-m,
由-1-m>0,得m<-1.
|
∴f(x)=(x+1)2;
(2)当x∈[-2,k]时,若-2≤k<-1,f(x)min=(k+1)2;
当x≥-1时,f(x)min=0.
∴f(x)min=
|
(3)令g(x)=f(x)-5x-m=x2-3x+1-m,x∈[-1,1],
则g′(x)=2x-3,
当x∈[-1,1]时g′(x)≤0恒成立,
∴g(x)在[-1,1]上为减函数,
g(x)min=1-3+1-m=-1-m,
由-1-m>0,得m<-1.
点评:本题考查了函数解析式的求解及常用方法,考查了二次函数最值得求法,训练了利用导数求函数的最值,体现了数学转化思想方法和分类讨论的数学思想方法,是压轴题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
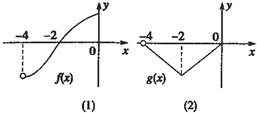 已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),它们在(-4,0]上的图象分别是图①和图②,则关于x的不等式f(x)•g(x)<0的解集是( )
已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),它们在(-4,0]上的图象分别是图①和图②,则关于x的不等式f(x)•g(x)<0的解集是( )| A、(-2,0)∪(2,4) |
| B、[0,4] |
| C、(2,4) |
| D、(-2,0] |
下列函数中,在区间(0,+∞)上为增函数的是( )
| A、y=ln(x+1) | ||
B、y=-
| ||
C、y=(
| ||
D、y=x+
|