题目内容
18．已知函数y=lnx-mx（m∈R）（1）若函数y=f（x）过点P（1，-1），求曲线y=f（x）在点P处的切线方程；
（2）求函数f（x）在区间[1，e]上的最大值．
分析 （1）根据导数的意义求解斜率，由点斜式得出方程即可；
（2）求出导函数，对参数m进行分类讨论，分别求出闭区间上的最大值．
解答 21、解：（1）因为点P（1，-1）在曲线y=f（x）上，所以-m=-1，解得m=1．
因为f'（x）=$\frac{1}{x}$-1=0，所以切线的斜率为0，所以切线方程为y=-1．----------------（5分）
（2）因为f'（x）=$\frac{1}{x}$-m=$\frac{1-mx}{x}$，
①当m≤0时，在区间[1，e]上，f'（x）＞0，
所以函数f（x）在[1，e]上单调递增，则最大值为f（e）=1-me；
②当$\frac{1}{m}$≥e，即0＜m≤$\frac{1}{e}$时，f'（x）＞0，
所以函数f（x）在[1，e]上单调递增，则最大值为f（e）=1-me；
③当1＜$\frac{1}{m}$＜e，即$\frac{1}{e}$＜m＜1，
函数f（x）在（1，$\frac{1}{m}$）上单调递增，在（$\frac{1}{m}$，e）上单调递减，则最大值f（$\frac{1}{m}$）=-lnm-1；
④当0＜$\frac{1}{m}$＜e，即m≥1时，f'（x）＜0，
函数f（x）在（1，e）上单调递减，则最大值f（1）=-m．．--------------------（10分）
综上，当m≤$\frac{1}{e}$时，最大值为1=me；当$\frac{1}{e}$＜m＜1时，则最大值-lnm-1；当m≥1时，最大值-m．．--------------------（12分）
点评 考查了导函数的意义和利用导函数求函数闭区间上的最值，难点是对参数的分类讨论．
练习册系列答案
步步高达标卷系列答案
相关题目
8．
如图，网格纸上的小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积是（ ）
如图，网格纸上的小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积是（ ）| A． | 4+6π | B． | 4+12π | C． | 8+6π | D． | 8+12π |
6．已知实数x，y满足$\left\{\begin{array}{l}x-2y+4≥0\\ 2x+y-2≥0\\ 3x-y-4≤0\end{array}\right.$，则z=x2+y2的最小值为（ ）
| A． | 1 | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{4}{5}$ | D． | 4 |
13．已知向量$\overrightarrow a=（-2，0），\overrightarrow a-\overrightarrow b=（-3，-1）$，则下列结论正确的是 （ ）
| A． | $\overrightarrow a•\overrightarrow b=2$ | B． | $\overrightarrow a∥\overrightarrow b$ | C． | $|\overrightarrow a|=|\overrightarrow b|$ | D． | $\overrightarrow b⊥（\overrightarrow a+\overrightarrow b）$ |
3．已知F为双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的左焦点，直线l经过点F，若点A（a，0），B（0，b）关于直线l对称，则双曲线C的离心率为（ ）
| A． | $\frac{{\sqrt{3}+1}}{2}$ | B． | $\frac{{\sqrt{2}+1}}{2}$ | C． | $\sqrt{3}+1$ | D． | $\sqrt{2}+1$ |
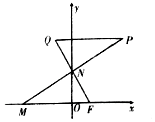已知点F（1，0），动点M，N分别在x轴，y轴上运动，MN⊥NF，Q为平面上一点，$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$，过点Q作QP平行于x轴交MN的延长线于点P．