题目内容
7.设向量$\overrightarrow{a}$=(1,2m),$\overrightarrow{b}$=(m+1,1),$\overrightarrow{c}$=(m,3),若($\overrightarrow{a}$+$\overrightarrow{c}$)⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$|=$\sqrt{17}$.分析 利用平面向量坐标运算法则求出$\overrightarrow{a}+\overrightarrow{c}$,再利用向量垂直的性质求出$\overrightarrow{a}$,由此能求出|$\overrightarrow{a}$|.
解答 解:∵向量$\overrightarrow{a}$=(1,2m),$\overrightarrow{b}$=(m+1,1),$\overrightarrow{c}$=(m,3),
∴$\overrightarrow{a}$+$\overrightarrow{c}$=(1+m,2m+3),
∵($\overrightarrow{a}$+$\overrightarrow{c}$)⊥$\overrightarrow{b}$,
∴(1+m)(m+1)+2m+3=0,
解得m=-2,
∴$\overrightarrow{a}$=(1,-4),
∴|$\overrightarrow{a}$|=$\sqrt{1+16}$=$\sqrt{17}$.
故答案为:$\sqrt{17}$.
点评 本题考查向量的模的求法,是基础题,解题时要认真审题,注意平面向量运算法则的合理运用.

练习册系列答案
相关题目
15.已知点A(4,4)在抛物线y2=2px (p>0)上,该抛物线的焦点为F,过点A作该抛物线准线的垂线,垂足为E,则∠EAF的平分线所在的直线方程为( )
| A. | 2x+y-12=0 | B. | x+2y-12=0 | C. | 2x-y-4=0 | D. | x-2y+4=0 |
2.复数z=$\frac{(1-i)^{2}}{1+i}$的共轭复数$\overline{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.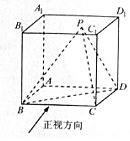 如图,在正方体ABC的-A1B1C1D1中,点P是线段A1C1上的动点,则三棱锥P-BCD的俯视图与正视图面积之比的最大值为( )
如图,在正方体ABC的-A1B1C1D1中,点P是线段A1C1上的动点,则三棱锥P-BCD的俯视图与正视图面积之比的最大值为( )
 如图,在正方体ABC的-A1B1C1D1中,点P是线段A1C1上的动点,则三棱锥P-BCD的俯视图与正视图面积之比的最大值为( )
如图,在正方体ABC的-A1B1C1D1中,点P是线段A1C1上的动点,则三棱锥P-BCD的俯视图与正视图面积之比的最大值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |