题目内容
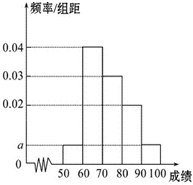 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100](1)求图中a的值并计算[70,100]的人数;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分.
考点:频率分布直方图
专题:概率与统计
分析:(1)由频率分布直方图知:2a=[1-(0.02+0.03+0.04)×10]÷10=0.01.由此能求出a.
故答案为:0.005.
(2)由频率分布直方图,能估计出这100名学生语文成绩的平均分.
故答案为:0.005.
(2)由频率分布直方图,能估计出这100名学生语文成绩的平均分.
解答:
解:(1)由频率分布直方图知:
2a=[1-(0.02+0.03+0.04)×10]÷10=0.01.
解得a=0.005.
故答案为:0.005.
(2)由频率分布直方图,
估计这100名学生语文成绩的平均分:
=0.005×10×55+0.04×10×65+0.03×10×75+0.02×10×85+0.005×10×95=73(分).
∴估计这100名学生语文成绩的平均分为73分.
2a=[1-(0.02+0.03+0.04)×10]÷10=0.01.
解得a=0.005.
故答案为:0.005.
(2)由频率分布直方图,
估计这100名学生语文成绩的平均分:
. |
| x |
∴估计这100名学生语文成绩的平均分为73分.
点评:本题考查频率分布直方图的应用,是基础题,解题时要认真审题.

练习册系列答案
相关题目
已知F1F2是椭圆C1:
+
=1与双曲线C2的公共焦点,点P是曲线C1与C2的一个公共点,且|
|=
(其中点O为坐标原点),则双曲线C2离心率为( )
| x2 |
| 9 |
| y2 |
| 5 |
| OP |
| ||
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
已知f′(x)为f(x)的导数,若f′(x)<f(x)对于任意的x∈R都成立,则( )
A、f(0)<
| ||
B、f(0)>
| ||
C、f(0)=
| ||
D、
|
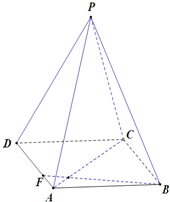 如图所示,正四棱锥P=ABCD中,AB=1,侧棱PA与底面ABCD所成角的正切值为
如图所示,正四棱锥P=ABCD中,AB=1,侧棱PA与底面ABCD所成角的正切值为