题目内容
已知F1F2是椭圆C1:
+
=1与双曲线C2的公共焦点,点P是曲线C1与C2的一个公共点,且|
|=
(其中点O为坐标原点),则双曲线C2离心率为( )
| x2 |
| 9 |
| y2 |
| 5 |
| OP |
| ||
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
考点:双曲线的简单性质
专题:综合题
分析:利用椭圆、双曲线的定义,结合余弦定理,即可得出结论.
解答:
解:设|
|=m,|
|=n,且m>n,<
,
>=θ,曲线C2:
-
=1,
由条件知|
|2=
(m2+n2+2mncosθ)=(
)2,
及三角形PF1F2中余弦定理m2+n2-2mncosθ=(2c)2=42,
结合m+n=6,m-n=2a可得a=
,从而e=
,
故选B.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
| x2 |
| a2 |
| y2 |
| b2 |
由条件知|
| OP |
| 1 |
| 4 |
| ||
| 3 |
及三角形PF1F2中余弦定理m2+n2-2mncosθ=(2c)2=42,
结合m+n=6,m-n=2a可得a=
| 4 |
| 3 |
| 3 |
| 2 |
故选B.
点评:本题考查椭圆、双曲线的定义,考查余弦定理,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知函数f(x)=ax2009+bsinx+1,且f(m)=2,则f(-m)=( )
| A、0 | B、1 | C、4 | D、-1 |
已知一门高射炮射击一次击中目标的概率是0.4,那么至少需要这样的高射炮多少门同时对某一目标射击一次,才能使该目标被击中的概率超过96%(提供的数据:lg2=0.30,lg3=0.48)( )
| A、5 | B、6 | C、7 | D、8 |
过双曲线x2-y2=1的右焦点且斜率是1的直线与双曲线的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
 若函数f(x)=Asin(2x+φ)(A>0,-
若函数f(x)=Asin(2x+φ)(A>0,-| π |
| 2 |
| π |
| 2 |
| A、-2 | ||
| B、-1 | ||
C、-
| ||
D、-
|
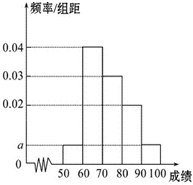 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]