题目内容
已知f′（x）为f（x）的导数，若f′（x）＜f（x）对于任意的x∈R都成立，则（ ）
A、f（0）＜
| ||
B、f（0）＞
| ||
C、f（0）=
| ||
D、
|
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：构造函数g（x）=
利用导数判断函数的单调性，即可得到结论．
| f(x) |
| ex |
解答：
解：由f′（x）＜f（x）得f′（x）-f（x）＜0，
构造函数g（x）=
，
则g′（x）=
=
＜0，即函数g（x）单调递减，
则g（2014）＜g（0），
即
＜
，
则f（0）＞
，
故选：B
构造函数g（x）=
| f(x) |
| ex |
则g′（x）=
| f′(x)ex-exf(x) |
| (ex)2 |
| f′(x)-f(x) |
| ex |
则g（2014）＜g（0），
即
| f(2014) |
| e2014 |
| f(0) |
| e0 |
则f（0）＞
| f(2014) |
| e2014 |
故选：B
点评：本题主要考查函数值的大小比较，根据条件构造函数是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
过双曲线x2-y2=1的右焦点且斜率是1的直线与双曲线的交点个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
若函数f（x）=Asin（2x+φ）（A＞0，-| π |
| 2 |
| π |
| 2 |
| A、-2 | ||
| B、-1 | ||
C、-
| ||
D、-
|
函数f（x）=2sin（ωx+φ）（ω＞0）的图象经过A（-
，-2）、B（
，2）两点，则ω（ ）
| π |
| 6 |
| π |
| 4 |
| A、最大值为3 | ||
| B、最小值为3 | ||
C、最大值为
| ||
D、最小值为
|
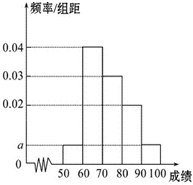某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]