题目内容
19.观察:$\sqrt{6}$+$\sqrt{15}$<2$\sqrt{11}$,$\sqrt{5.5}$+$\sqrt{15.5}$<2$\sqrt{11}$,$\sqrt{4-\sqrt{2}}$+$\sqrt{17+\sqrt{2}}$<2$\sqrt{11}$,…,对于任意的正实数a,b,使$\sqrt{a}$+$\sqrt{b}$<2$\sqrt{11}$成立的一个条件可以是( )| A. | a+b=22 | B. | a+b=21 | C. | ab=20 | D. | ab=21 |
分析 观察前三个不等式的特点,归纳出来不等式的规律,即可得到结论.
解答 解:∵6+15=5.5+15.5=4-$\sqrt{2}$+17+$\sqrt{2}$=21,
∴根据归纳推理的知识,可以猜想满足$\sqrt{a}$+$\sqrt{b}$<2$\sqrt{11}$成立的一个条件可以是a+b=21.
故选B.
点评 本题主要考查归纳推理的应用,根据不等式的特点归纳出规律是解决本题的关键,比较基础.

练习册系列答案
相关题目
8.已知等边三角形的边长为1,那么它的平面直观图面积为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{8}$ | C. | $\frac{\sqrt{6}}{8}$ | D. | $\frac{\sqrt{6}}{16}$ |
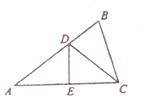 如图,设△ABC的三个内角A,B,C对应的三条边分别为a,b,c,且角A,B,C成等差数列,a=2,线段AC的垂直平分线分别交线段AB,AC于D,E两点.
如图,设△ABC的三个内角A,B,C对应的三条边分别为a,b,c,且角A,B,C成等差数列,a=2,线段AC的垂直平分线分别交线段AB,AC于D,E两点.