题目内容
已知函数f(x)=xlnx.
(1)若函数g(x)=f(x)+x2+ax+2有零点,求实数a的范围;
(2)若f(x)≥k(x+1)(k∈Z)恒成立,求k的最大值.
(1)若函数g(x)=f(x)+x2+ax+2有零点,求实数a的范围;
(2)若f(x)≥k(x+1)(k∈Z)恒成立,求k的最大值.
考点:函数恒成立问题
专题:导数的综合应用
分析:(1)把函数f(x)的解析式代入g(x)=f(x)+x2+ax+2,分离参数a得到-a=lnx+x+
,把函数有零点转化为次方程在(0,+∞)上有实数根,构造函数h(x)=lnx+x+
,求出此函数在(0,+∞)上的最小值,由-a大于函数的最小值求解a的范围;
(2)把f(x)的解析式代入f(x)≥k(x+1),分离变量k,把不等式恒成立转化为k≤
恒成立,由导数求出函数y=
的最小值,则整数k的最大值可求.
| 2 |
| x |
| 2 |
| x |
(2)把f(x)的解析式代入f(x)≥k(x+1),分离变量k,把不等式恒成立转化为k≤
| xlnx |
| x+1 |
| xlnx |
| x+1 |
解答:
解:(1)∵函数g(x)=f(x)+x2+ax+2有零点,
∴g(x)=xlnx+x2+ax+2在(0,+∞)上有实数根.
即-a=lnx+x+
在(0,+∞)上有实数根.
令h(x)=lnx+x+
,(x>0),则h′(x)=
+1-
=
.
解h′(x)<0,得0<x<1,此时函数递减;
解h′(x)>0,得x>1,此时函数递增.
∴h(x)在x=1时取得极小值,同时也是最小值,
即最小值h(1)=3.
∴-a≥3,
解得a≤-3;
(2)f(x)≥k(x+1)(k∈Z)恒成立,则k≤
,
令y=
,y′=
,
令m(x)=lnx+x+1,则m′(x)=
+1>0,
∴m(x)=lnx+x+1在(0,+∞)上单调递增.
∵m(e-2)<0,m(e-1)>0,
∴在(
,
)内存在一点x0,使得m(x0)=0.
∴当x∈(0,x0)时,y′<0,函数y=
为减函数,
当x∈(x0,+∞)时,y′>0,函数y=
为增函数,
∴当x=x0时函数y=
有最小值.
最小值为
∈(
,
)=(-
,-
).
∵k≤
,
∴k的最大值为-1.
∴g(x)=xlnx+x2+ax+2在(0,+∞)上有实数根.
即-a=lnx+x+
| 2 |
| x |
令h(x)=lnx+x+
| 2 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| x2+x-1 |
| x2 |
解h′(x)<0,得0<x<1,此时函数递减;
解h′(x)>0,得x>1,此时函数递增.
∴h(x)在x=1时取得极小值,同时也是最小值,
即最小值h(1)=3.
∴-a≥3,
解得a≤-3;
(2)f(x)≥k(x+1)(k∈Z)恒成立,则k≤
| xlnx |
| x+1 |
令y=
| xlnx |
| x+1 |
| lnx+x+1 |
| (x+1)2 |
令m(x)=lnx+x+1,则m′(x)=
| 1 |
| x |
∴m(x)=lnx+x+1在(0,+∞)上单调递增.
∵m(e-2)<0,m(e-1)>0,
∴在(
| 1 |
| e2 |
| 1 |
| e |
∴当x∈(0,x0)时,y′<0,函数y=
| xlnx |
| x+1 |
当x∈(x0,+∞)时,y′>0,函数y=
| xlnx |
| x+1 |
∴当x=x0时函数y=
| xlnx |
| x+1 |
最小值为
| x0lnx0 |
| x0+1 |
| ||||
|
| ||||
|
| 2 |
| 1+e2 |
| 1 |
| 1+e |
∵k≤
| xlnx |
| x+1 |
∴k的最大值为-1.
点评:本题考查了函数恒成立问题,考查了分离变量法、函数构造法以及利用导数求函数的最值,属难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
角α终边上有一点(-1,2),则下列各点中在角2α的终边上的点是( )
| A、(3,4) |
| B、(-3,-4) |
| C、(4,3) |
| D、(-4,-3) |
已知α:|z|≤1,z∈C,β:|z-i|≤a,z∈C.若α是β的充分非必要条件,则实数a的取值范围是( )
| A、a≥1 | B、a≤1 |
| C、a≥2 | D、a≤2 |
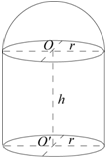 要设计一个金属容积为V(常数)的密闭容器,下部是圆柱形,上部为半球形(如图).当圆柱底面半径r与高h各为何值时,制造这个容器用料最省(表面积最小)?
要设计一个金属容积为V(常数)的密闭容器,下部是圆柱形,上部为半球形(如图).当圆柱底面半径r与高h各为何值时,制造这个容器用料最省(表面积最小)?