题目内容
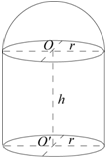要设计一个金属容积为V（常数）的密闭容器，下部是圆柱形，上部为半球形（如图）．当圆柱底面半径r与高h各为何值时，制造这个容器用料最省（表面积最小）？考点：基本不等式在最值问题中的应用
专题：应用题,不等式的解法及应用
分析：由题意V=πr2h+
πr3，S表=3πr2+2πrh，化简可得S表=
πr2+
，利用基本不等式，即可求得结论．
| 2 |
| 3 |
| 5 |
| 3 |
| 2V |
| r |
解答：
解：V=πr2h+
πr3①，S表=3πr2+2πrh②
由①可得h=
，
代入②S表=3πr2+2πr•
=
πr2+
．…（6分）
=
πr2+
+
≥3
=3
，
当且仅当
πr2=
即r=
时S表最小．…（10分）
此时h=
即r=h=
时用料最省．…（12分）
| 2 |
| 3 |
由①可得h=
V-
| ||
| πr2 |
代入②S表=3πr2+2πr•
V-
| ||
| πr2 |
| 5 |
| 3 |
| 2V |
| r |
=
| 5 |
| 3 |
| V |
| r |
| V |
| r |
| 3 | (
| ||||
| 3 |
| ||
当且仅当
| 5 |
| 3 |
| V |
| r |
| 3 |
| ||
此时h=
| 3 |
| ||
| 3 |
| ||
点评：本题考查基本不等式在最值问题中的应用，求得表面积是关键．
练习册系列答案
阅读快车系列答案
相关题目
等比数列的前n项，前2n项，前3n项的和分别是A，B，C，则（ ）
| A、（A+B）-C=B2 |
| B、A2+B2=A（B+C） |
| C、A+B=C |
| D、B2=AC |
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示，其中甲成绩的中位数为15，极差为12；乙成绩的众数为13，. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中，a=4，b=6
，A=30°，则此三角形解的情况是 （ ）
| 2 |
| A、一解 | B、两解 |
| C、一解或两解 | D、无解 |
如图，把边长为10的正六边形纸板剪去相同的六个角，做成一个底面为正六边形的无盖六棱柱盒子，设其高为h，体积为V（不计接缝）．