题目内容
17.已知数列{an}满足$\frac{1}{lg(1-\sqrt{{a}_{1}})}$+$\frac{2}{lg(1-\sqrt{{a}_{2}})}$+…+$\frac{n}{lg(1-\sqrt{{a}_{n}})}$=-$\frac{n}{lg2}$(n≥1).(1)求数列{an}的通项公式;
(2)对于任意实数x和正整数n,
(Ⅰ)证明:$\frac{{a}_{n}}{n}$≥x($\frac{1}{{2}^{0}}$-x)+x($\frac{1}{2}$-x)+x($\frac{1}{{2}^{2}}$-x)+…+x($\frac{1}{{2}^{n-1}}$-x);
(Ⅱ)证明:$\frac{{a}_{1}}{1}$+$\frac{{a}_{2}}{2}$+…+$\frac{{a}_{n}}{n}$>$\frac{2(n-1)^{2}}{n(n+1)}$.
分析 (1)通过$\frac{1}{lg(1-\sqrt{{a}_{1}})}$+$\frac{2}{lg(1-\sqrt{{a}_{2}})}$+…+$\frac{n}{lg(1-\sqrt{{a}_{n}})}$=-$\frac{n}{lg2}$与$\frac{1}{lg(1-\sqrt{{a}_{1}})}$+$\frac{2}{lg(1-\sqrt{{a}_{2}})}$+…+$\frac{n-1}{lg(1-\sqrt{{a}_{n-1}})}$=-$\frac{n-1}{lg2}$(n≥2)作差,整理得an=1-$\frac{1}{{2}^{n-1}}$+$\frac{1}{{4}^{n}}$(n≥2),进而可得结论;
(2)(Ⅰ)由(1)可知an=$(1-\frac{1}{{2}^{n}})^{2}$,利用分组法求和及基本不等式可知结论成立;(Ⅱ)由(I)及柯西不等式整理即得结论.
解答 (1)解:∵$\frac{1}{lg(1-\sqrt{{a}_{1}})}$+$\frac{2}{lg(1-\sqrt{{a}_{2}})}$+…+$\frac{n}{lg(1-\sqrt{{a}_{n}})}$=-$\frac{n}{lg2}$(n≥1),
∴$\frac{1}{lg(1-\sqrt{{a}_{1}})}$+$\frac{2}{lg(1-\sqrt{{a}_{2}})}$+…+$\frac{n-1}{lg(1-\sqrt{{a}_{n-1}})}$=-$\frac{n-1}{lg2}$(n≥2),
两式相减得:$\frac{n}{lg(1-\sqrt{{a}_{n}})}$=$\frac{n-1}{lg2}$-$\frac{n}{lg2}$,
整理得:an=1-$\frac{1}{{2}^{n-1}}$+$\frac{1}{{4}^{n}}$(n≥2),
又∵$\frac{1}{lg(1-\sqrt{{a}_{1}})}$=-$\frac{1}{lg2}$,即a1=$\frac{1}{4}$满足上式,
∴数列{an}的通项公式an=1-$\frac{1}{{2}^{n-1}}$+$\frac{1}{{4}^{n}}$;
(2)证明:(Ⅰ)由(1)可知,an=$(1-\frac{1}{{2}^{n}})^{2}$,
则x($\frac{1}{{2}^{0}}$-x)+x($\frac{1}{2}$-x)+x($\frac{1}{{2}^{2}}$-x)+…+x($\frac{1}{{2}^{n-1}}$-x)
=x($\frac{1}{{2}^{0}}$+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-nx)
=x•($\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-nx)
=x[2(1-$\frac{1}{{2}^{n}}$)-nx]
=$\frac{1}{n}$•nx[2(1-$\frac{1}{{2}^{n}}$)-nx]
≤$\frac{(1-\frac{1}{{2}^{n}})^{2}}{n}$,
即$\frac{{a}_{n}}{n}$≥x($\frac{1}{{2}^{0}}$-x)+x($\frac{1}{2}$-x)+x($\frac{1}{{2}^{2}}$-x)+…+x($\frac{1}{{2}^{n-1}}$-x);
(Ⅱ)由(I)可知,$\frac{{a}_{n}}{n}$≥$\frac{(1-\frac{1}{{2}^{n}})^{2}}{n}$,
∴$\frac{{a}_{1}}{1}$+$\frac{{a}_{2}}{2}$+…+$\frac{{a}_{n}}{n}$≥$\frac{[(1-\frac{1}{2})+(1-\frac{1}{{2}^{2}})+…+(1-\frac{1}{{2}^{n}})]^{2}}{1+2+3+…+n}$
=$\frac{[{n-\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}]}^{2}}{\frac{n(n+1)}{2}}$
=$\frac{2(n-1+\frac{1}{{2}^{n}})^{2}}{n(n+1)}$
>$\frac{2(n-1)^{2}}{n(n+1)}$.
点评 本题考查数列的通项及前n项和,考查不等式,涉及基本不等式及柯西不等式等基础知识,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于难题.

| A. | 0 | B. | 2015 | C. | 2016 | D. | 2017 |
| A. | 若a>0,则a>1 | B. | 若a≤0,则a>1 | C. | 若a>0,则a≤1 | D. | 若a≤0,则a≤1 |
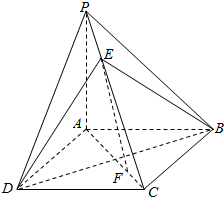 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,点E、F在PC、AC上,PE=$\frac{1}{4}$PC.
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,点E、F在PC、AC上,PE=$\frac{1}{4}$PC.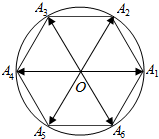 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.