题目内容
12.若f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则f(x)<0的解集是{x|x<-3或0<x<3}.分析 利用函数是奇函数且在(0,+∞)内是增函数,得到函(-∞,0)上单调递增,利用f(-3)=0,得f(3)=0,然后解不等式即可.
解答  解:∵f(x)是奇函数,f(-3)=0,
解:∵f(x)是奇函数,f(-3)=0,
∴f(-3)=-f(3)=0,解f(3)=0.
∵函数在(0,+∞)内是增函数,
∴当0<x<3时,f(x)<0.
当x>3时,f(x)>0,
∵函数f(x)是奇函数,
∴当-3<x<0时,f(x)>0.
当x<-3时,f(x)<0,
则不等式f(x)<0的解集{x|x<-3或0<x<3}.
故答案为:{x|x<-3或0<x<3}
点评 本题主要考查函数奇偶性和单调性之间的关系,利用函数奇偶性的对称性,可解不等式的解集.

练习册系列答案
相关题目
2.过双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作圆C2:x2+y2=a2的切线,设切点为M,延长FM交双曲线C1于点N,若点M为线段FN的中点,则双曲线C1的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$+1 | D. | $\frac{\sqrt{5}+1}{2}$ |
1.已知某圆锥曲线C的极坐标方程是ρ2=$\frac{225}{9+16co{s}^{2}θ}$,则曲线C的离心率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
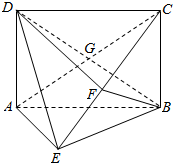 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.