题目内容
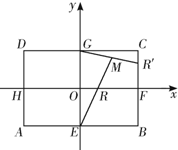 如图,矩形ABCD中,|AB|=2
如图,矩形ABCD中,|AB|=2| 2 |
| OR |
| OF |
| CR′ |
| CF |
(Ⅰ)求证:直线ER与GR′的交点M在椭圆Γ:
| x2 |
| 2 |
(Ⅱ)若点N是直线l:y=x+2上且不在坐标轴上的任意一点,F1、F2分别为椭圆Γ的左、右焦点,直线NF1和NF2与椭圆Γ的交点分别为P、Q和S、T.是否存在点N,使得直线OP、OQ、OS、OT的斜率kOP、kOQ、kOS、kOT满足kOP+kOQ+kOS+kOT=0?若存在,求出点N的坐标;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知,得F(
,0),C(
,1),R(
λ,0),R′(
,1-λ),E(0,-1),G(0,1),由此求出直线ER的方程和直线GR′的方程,从而能够证明直线ER与GR′的交点为M在椭圆Γ上.
(Ⅱ)假设满足条件的点N(x0,y0)存在,则直线NF1:y=k1(x+1),直线NF2:y=k2(x-1),由
,求出kOP+kOQ=-
.同理,kOS+kOT=-
,由此能求出满足条件的点N存在,其坐标为(-
,
).
| 2 |
| 2 |
| 2 |
| 2 |
(Ⅱ)假设满足条件的点N(x0,y0)存在,则直线NF1:y=k1(x+1),直线NF2:y=k2(x-1),由
|
| 2k1 |
| k12-1 |
| 2k2 |
| k22-1 |
| 5 |
| 4 |
| 3 |
| 4 |
解答:
(本小题满分13分)
(Ⅰ)证明:由已知,得F(
,0),C(
,1).
由
=λ
,
=λ
,得R(
λ,0),R′(
,1-λ).
又E(0,-1),G(0,1),则
直线ER的方程为y=
x-1,①
直线GR′的方程为y=-
x+1. ②
由①②,得M(
,
).
∵
+(
)2=
=
=1,
∴直线ER与GR′的交点为M在椭圆Γ:
+y2=1上.
(Ⅱ)解:假设满足条件的点N(x0,y0)存在,
则直线NF1:y=k1(x+1),其中k1=
,
直线NF2:y=k2(x-1),其中k2=
,
由
,消去y并化简,得(2k12+1)x2+4k12x+2k12-2=0,
设P(x1,y1),Q(x2,y2),则x1+x2=-
,x1x2=
,
∵OP,OQ的斜率存在,∴x1≠0,x2≠0,∴k12≠1,
∴kOP+kOQ=
+
=
+
=2k1+k1•
=k1(2-
)=-
.
同理,得kOS+kOT=-
,
∴kOP+kOQ+kOS+kOT
=-2(
+
)
=-2•
=-
,
∵kOP+kOQ+kOS+kOT=0,
∴-
=0,即(k1+k2)(k1k2-1)=0,
由点N不在坐标轴上,知k1+k2≠0,
∴k1k2=1,即
•
=1,③
又y0=x0+2,④
解③④得x0=-
,y0=
,
∴满足条件的点N存在,其坐标为(-
,
).
(Ⅰ)证明:由已知,得F(
| 2 |
| 2 |
由
| OR |
| OF |
| CR′ |
| CF |
| 2 |
| 2 |
又E(0,-1),G(0,1),则
直线ER的方程为y=
| 1 | ||
|
直线GR′的方程为y=-
| λ | ||
|
由①②,得M(
2
| ||
| 1+λ2 |
| 1-λ2 |
| 1+λ2 |
∵
[
| ||||
| 2 |
| 1-λ2 |
| 1+λ2 |
| 4λ2+(1-λ2)2 |
| (1+λ2)2 |
| (1+λ2)2 |
| (1+λ2)2 |
∴直线ER与GR′的交点为M在椭圆Γ:
| x2 |
| 2 |
(Ⅱ)解:假设满足条件的点N(x0,y0)存在,
则直线NF1:y=k1(x+1),其中k1=
| y0 |
| x0+1 |
直线NF2:y=k2(x-1),其中k2=
| y0 |
| x0-1 |
由
|
设P(x1,y1),Q(x2,y2),则x1+x2=-
| 4k12 |
| 2k12+1 |
| 2k12-2 |
| 2k12+1 |
∵OP,OQ的斜率存在,∴x1≠0,x2≠0,∴k12≠1,
∴kOP+kOQ=
| y1 |
| x1 |
| y2 |
| x2 |
| k1(x1+1) |
| x1 |
| k1(x2+1) |
| x2 |
=2k1+k1•
| x1+x2 |
| x1x2 |
| 4k12 |
| 2k12-2 |
| 2k1 |
| k12-1 |
同理,得kOS+kOT=-
| 2k2 |
| k22-1 |
∴kOP+kOQ+kOS+kOT
=-2(
| k1 |
| k12-1 |
| k2 |
| k22-1 |
=-2•
| k1k22-k1+k12k2-k2 |
| (k12-1)(k22-1) |
=-
| 2(k1+k2)(k1k2-1) |
| (k12-1)(k22-1) |
∵kOP+kOQ+kOS+kOT=0,
∴-
| 2(k1+k2)(k1k2-1) |
| (k12-1)(k22-1) |
由点N不在坐标轴上,知k1+k2≠0,
∴k1k2=1,即
| y0 |
| x0+1 |
| y0 |
| x0-1 |
又y0=x0+2,④
解③④得x0=-
| 5 |
| 4 |
| 3 |
| 4 |
∴满足条件的点N存在,其坐标为(-
| 5 |
| 4 |
| 3 |
| 4 |
点评:本题考查两直线交点在椭圆上的证明,考查满足条件的点是否存在的判断与求法,解题时要认真审题,注意直线斜率公式的灵活运用.

练习册系列答案
相关题目
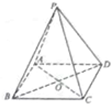 如图,三棱锥P-ABCD的底面ABCD是正方形,顶点P在底面的射影是AC与BD的交点O,AB=2,∠PAC=60°.
如图,三棱锥P-ABCD的底面ABCD是正方形,顶点P在底面的射影是AC与BD的交点O,AB=2,∠PAC=60°.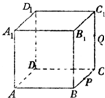 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=