题目内容
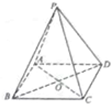 如图,三棱锥P-ABCD的底面ABCD是正方形,顶点P在底面的射影是AC与BD的交点O,AB=2,∠PAC=60°.
如图,三棱锥P-ABCD的底面ABCD是正方形,顶点P在底面的射影是AC与BD的交点O,AB=2,∠PAC=60°.(Ⅰ)求侧面PBC与底面ABCD所成的锐二面角的正切值;
(Ⅱ)在线段PB上是否存在一点E,使得AE⊥PC,若存在,试确定点E的位置,并加以证明;若不存在,请说明理由.
考点:与二面角有关的立体几何综合题,棱锥的结构特征
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出∠PMO为侧面与底面所成二面角平面角,由此能求出侧面PBC与底面ABCD所成的锐二面角的正切值.
(2)以O为原点建立空间O-xyz,利用向量法能求出存在点E,且点E分PB的比为2时,满足AE⊥PC.
(2)以O为原点建立空间O-xyz,利用向量法能求出存在点E,且点E分PB的比为2时,满足AE⊥PC.
解答:
 解:(Ⅰ)如图,O为底面ABCD的中心,
解:(Ⅰ)如图,O为底面ABCD的中心,
则∠PAO为PA与底面所成的角,
∴∠PAO=60°,
∵AO=
,∴PO=
,PA=2
,
过O作OM⊥BC于M,连结PM,
由三垂线定理,得BC⊥PM,
∴∠PMO为侧面与底面所成二面角平面角,
∵OM=1,PO=
,
∴tan∠PMO=
,
∴侧面PBC与底面ABCD所成的锐二面角的正切值为
.
(2)如图,以O为原点建立空间O-xyz,
则A(0,-
,0),C(0,
,0),P(0,0,
),B(
,0,0),
假设在PB上存在一点E,满足条件,设E分PB的比为r,
则E(
,0,
),
∴
=(
,
,
),
=(0,
,-
),
∵AE⊥PC,∴2-
=0,解得r=2.
∴存在点E,且点E分PB的比为2时,满足AE⊥PC.
 解:(Ⅰ)如图,O为底面ABCD的中心,
解:(Ⅰ)如图,O为底面ABCD的中心,则∠PAO为PA与底面所成的角,
∴∠PAO=60°,
∵AO=
| 2 |
| 6 |
| 2 |
过O作OM⊥BC于M,连结PM,
由三垂线定理,得BC⊥PM,
∴∠PMO为侧面与底面所成二面角平面角,
∵OM=1,PO=
| 6 |
∴tan∠PMO=
| 6 |
∴侧面PBC与底面ABCD所成的锐二面角的正切值为
| 6 |
(2)如图,以O为原点建立空间O-xyz,
则A(0,-
| 2 |
| 2 |
| 6 |
| 2 |
假设在PB上存在一点E,满足条件,设E分PB的比为r,
则E(
| ||
| 1+r |
| ||
| 1+r |
∴
| AE |
| ||
| 1+r |
| 2 |
| ||
| 1+r |
| PC |
| 2 |
| 6 |
∵AE⊥PC,∴2-
| 6 |
| 1+r |
∴存在点E,且点E分PB的比为2时,满足AE⊥PC.
点评:本题考查直线与平面所成角的正切值的求法,考查满足条件的点是否存在的判断所求法,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
设f(x)=sin(2x+
)+cos(2x+
),则函数f(x)( )
| π |
| 4 |
| π |
| 4 |
A、图象关于直线x=
| ||
B、图象关于直线x=
| ||
C、图象关于直线x=
| ||
D、图象关于直线x=
|
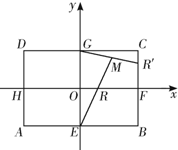 如图,矩形ABCD中,|AB|=2
如图,矩形ABCD中,|AB|=2