题目内容
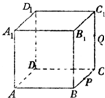 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=| 3 |
| 4 |
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:由题意作出满足条件的图形,由线面位置关系找出截面可得答案.
解答:
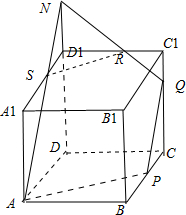 解:当CQ=
解:当CQ=
时,如图,
延长DD1至N,使D1N=
,
连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,故可得C1R=
,
故答案为:
 解:当CQ=
解:当CQ=| 3 |
| 4 |
延长DD1至N,使D1N=
| 1 |
| 2 |
连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,故可得C1R=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查的知识点是棱柱的几何特征,其中画出满足条件的图象,是解答的关键.

练习册系列答案
相关题目
不等式组
所表示的平面区域的面积为( )
|
A、
| ||
| B、2 | ||
C、
| ||
D、
|
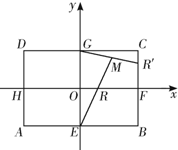 如图,矩形ABCD中,|AB|=2
如图,矩形ABCD中,|AB|=2