题目内容

已知集合A={a，b}，集合B={c，d，e}．
（1）试建立一个由A到B的映射；
（2）由A到B的映射共有多少个？
（3）由（1），（2）你能否得出一个结论？
考点：映射
专题：函数的性质及应用
分析：（1）根据映射的定义，结合集合A={a，b}，集合B={c，d，e}，可写出一个满足条件的A到B的映射；
（2）由card（A）=2，card（B）=3，可得从A到B的映射的个数为9个，
（3）结合（1），（2）的结论和映射的定义，可得当非空集合A中有m个元素，B中有n个元素时，由A到B的映射共有nm个．
解答： 解：（1）∵集合A={a，b}，集合B={c，d，e}．
故由A到B的映射可以是：a→c，b→c，
（2）∵card（A）=2，card（B）=3，
则从A到B的映射的个数为card（B）card（A）=32=9个
（3）（1），（2）得：
当非空集合A中有m个元素，B中有n个元素时，
由A到B的映射共有nm个．
点评：本题考查的知识点是映射，熟练掌握映射的定义是解答的关键．
练习册系列答案
相关题目
已知数列{an}满足a1=2，向量
a
=（2，-1），
b
=（an+2n，an+1）且
a
⊥
b
．
（Ⅰ）求证数列{
an
2n
}为等差数列，并求{an}通项公式；
（Ⅱ）设bn=
an
n(n+1)2
，若对任意n∈N*都有bn＞
m2-3m
9
成立，求实数m的取值范围．
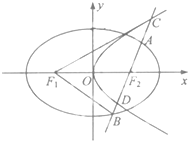设椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的上顶点为B1，左、右焦点为F1、F2，且F2和抛物线C2：y2=4x的焦点重合，△F1B1F2是正三角形．
（1）求椭圆C1的方程；
（2）过F2作直线l，与C1交于A、B两点，与C2交于C、D两点，求
S△F1CD
S△F1AB
的最小值．
已知函数f（x）=
x2+2x+3(x≤0)
x2eax(x＞0)

（Ⅰ）若a=-1，求函数f（x）的单调递增区间；
（Ⅱ）对任意的正实数m，关于x的方程f（x）=m恒有实数解，求实数a的取值范围．
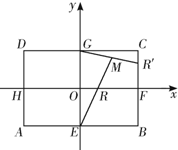如图，矩形ABCD中，|AB|=2
2
，|BC|=2．E，F，G，H分别是矩形四条边的中点，分别以HF，EG所在的直线为x轴，y轴建立平面直角坐标系，已知
OR
=λ
OF
，
CR′
=λ
CF
，其中0＜λ＜1．
（Ⅰ）求证：直线ER与GR′的交点M在椭圆Γ：
x2
2
+y2=1上；
（Ⅱ）若点N是直线l：y=x+2上且不在坐标轴上的任意一点，F1、F2分别为椭圆Γ的左、右焦点，直线NF1和NF2与椭圆Γ的交点分别为P、Q和S、T．是否存在点N，使得直线OP、OQ、OS、OT的斜率kOP、kOQ、kOS、kOT满足kOP+kOQ+kOS+kOT=0？若存在，求出点N的坐标；若不存在，请说明理由．
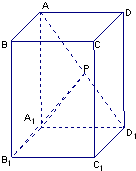已知ABCD-A1B1C1D1是底面为正方形的长方体，∠AD1A1=60°，AD1=4，点P是AD1上的动点．
（1）求证：不论点P在AD1上的任何位置，平面B1PA1都垂直于平面AA1D1
（2）当P为AD1的中点时，求异面直线AA1与B1P所成角的余弦值．
正方体的棱长为1，画过正方体AC1棱AA1，B1C1，A1B1上三个中点N，L，R的截面，并求截面面积．
（1）求证：函数f（x）=2x+2-x在[0，+∞）上是单调递增函数；
（2）求函数f（x）=2x+2-x（x∈R）的值域；
（3）设函数g（x）=
4x+2x+k+1
4x+2x+1+1
，若对任意的实数x1，x2，x3，都有g（x1）+g（x2）≥g（x3），求实数k的取值范围．
设x=
2+
3
2-
3
，y=
2-
3
2+
3
，则x3+y3=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网