题目内容
比较ln(x4+1)与ln(x2+1)的大小.
考点:对数值大小的比较
专题:常规题型,不等式的解法及应用
分析:要比较ln(x4+1)与ln(x2+1)的大小,由于底数为e>1,只需比较x4+1与x2+1的大小即可,用作差法比较.
解答:
解:∵x4+1-(x2+1)=x2(x2-1),
=x2(x+1)(x-1),
①当x=±1或x=0时,x4+1=x2+1,
∴ln(x4+1)=ln(x2+1);
②当x<-1或x>1时,x4+1>x2+1,
∴ln(x4+1)>ln(x2+1),
③当-1<x<0或0<x<1时,x4+1<x2+1,
∴ln(x4+1)<ln(x2+1).
=x2(x+1)(x-1),
①当x=±1或x=0时,x4+1=x2+1,
∴ln(x4+1)=ln(x2+1);
②当x<-1或x>1时,x4+1>x2+1,
∴ln(x4+1)>ln(x2+1),
③当-1<x<0或0<x<1时,x4+1<x2+1,
∴ln(x4+1)<ln(x2+1).
点评:本题考查了对数式比较大小,解答时转化成比较真数的大小,在利用作差法比较大小时注意分类讨论.

练习册系列答案
相关题目
抛物线y=8x2的焦点坐标为( )
A、(0,
| ||
B、(
| ||
| C、(2,0) | ||
| D、(0,2) |
把曲线ysinx-2y+3=0先沿x轴向左平移
个单位长度,再沿y轴向下平移1个单位长度,得到曲线方程是( )
| π |
| 2 |
| A、(1-y)cosx+2y-3=0 |
| B、(1+y)sinx-2y+1=0 |
| C、(1+y)cosx-2y+1=0 |
| D、-(1+y)cosx+2y+1=0 |
 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底ABCD,且PD=CD,点M、N分别是被AD、PC的中点,
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底ABCD,且PD=CD,点M、N分别是被AD、PC的中点,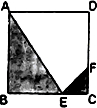 某人定制了一批地砖,每块地转(如图所示)是边长为1米的正方形ABCD,点EF分别在边BC和CD上,且CE=CF,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元.问点E在什么位置时,每块地转所需的材料费用最省?
某人定制了一批地砖,每块地转(如图所示)是边长为1米的正方形ABCD,点EF分别在边BC和CD上,且CE=CF,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元.问点E在什么位置时,每块地转所需的材料费用最省?