题目内容
已知{an}为递增的等比数列,且{a1,a3,a5}⊆{-10,-6,-2,0,1,3,4,16}.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若等差数列{bn}的通项公式为bn=n,求Sn=a1bn+a2bn-1+…+anb1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若等差数列{bn}的通项公式为bn=n,求Sn=a1bn+a2bn-1+…+anb1.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由已知得数列{an}的公比是正数,由a1=1,a3=4,a5=16,得q=2,由此能求出an=2n-1.
(Ⅱ)由等差数列{bn}的通项公式为bn=n,得Sn=1×n+2(n-1)+22(n-2)+23(n-3)+…+2n-2×2+2n-1×1,由此利用错位相减法能求出Sn.
(Ⅱ)由等差数列{bn}的通项公式为bn=n,得Sn=1×n+2(n-1)+22(n-2)+23(n-3)+…+2n-2×2+2n-1×1,由此利用错位相减法能求出Sn.
解答:
解:(Ⅰ)∵{an}为递增的等比数列,
∴数列{an}的公比是正数,
又{a1,a3,a5}⊆{-10,-6,-2,0,1,3,4,16},
∴a1=1,a3=4,a5=16,
从而q2=
=4,解得q=2,an=a1qn-1=2n-1,
∴an=2n-1.
(Ⅱ)∵等差数列{bn}的通项公式为bn=n,
Sn=a1bn+a2bn-1+…+anb1.
∴Sn=1×n+2(n-1)+22(n-2)+23(n-3)+…+2n-2×2+2n-1×1,①
2Sn=2n+22(n-2)+23(n-2)+…+2n-1×2+2n×1,
②-①,得:
Sn=-n+2+22+23+…+2n-1+2n
=-n+
=2n+1-n-2.
∴数列{an}的公比是正数,
又{a1,a3,a5}⊆{-10,-6,-2,0,1,3,4,16},
∴a1=1,a3=4,a5=16,
从而q2=
| a5 |
| a3 |
∴an=2n-1.
(Ⅱ)∵等差数列{bn}的通项公式为bn=n,
Sn=a1bn+a2bn-1+…+anb1.
∴Sn=1×n+2(n-1)+22(n-2)+23(n-3)+…+2n-2×2+2n-1×1,①
2Sn=2n+22(n-2)+23(n-2)+…+2n-1×2+2n×1,
②-①,得:
Sn=-n+2+22+23+…+2n-1+2n
=-n+
| 2(1-2n) |
| 1-2 |
=2n+1-n-2.
点评:本题考查数列{an}的通项公式的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
下列说法正确的是( )
A、向量
| ||||
| B、两个有共同起点长度相等的向量,则终点相同 | ||||
| C、零向量没有方向 | ||||
| D、任一向量与零向量平行 |
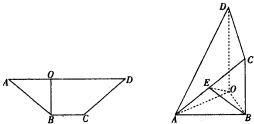 在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.
在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.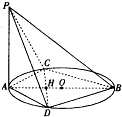 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面