题目内容
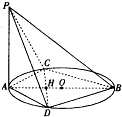 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面(Ⅰ)求证:PB⊥CD;
(Ⅱ)若PB=2
| 2 |
| π |
| 4 |
| 2π |
| 3 |
考点:点、线、面间的距离计算,直线与平面垂直的性质
专题:计算题,证明题,空间位置关系与距离
分析:(Ⅰ)由AB是圆O的直径知∠ACB=∠ADB=90°,从而证明PB⊥CD.(Ⅱ)过点P作PB的垂线,过点H作PB的垂线,分别交PB于点E,F;求出H到平面PBD的距离.
解答:
解:(Ⅰ)证明:∵AB是圆O的直径,
∴∠ACB=∠ADB=90°,
∵AC=AD,∴Rt△ACB≌Rt△ADB,∴AB⊥CD,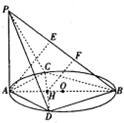
又∵PA⊥圆o所在平面,CD在圆o所在平面内,
∴PA⊥CD,
∵PA∩AB=A,∴CD⊥平面PAB,
∴PB⊥CD.
(Ⅱ)解:过点A作PB的垂线,过点H作PB的垂线,分别交PB于点E,F;
∵Rt△PAB中,∠PBA=45°,PB=2
,
∴PA=AB=2,∴AE=ABsin45°=
,
又∵∠CAB=∠DAB=60°,∴AC=AD=1,
∵CH⊥AH,∴AH=
,
∴BH=
,HD=
,BD=
,PD=
∴VH-PBD=VP-HDB=
×
×
×
×2=
,
S△PBD=
×
×
=
,
∴H到平面PBD的距离为
=
.
∴∠ACB=∠ADB=90°,
∵AC=AD,∴Rt△ACB≌Rt△ADB,∴AB⊥CD,

又∵PA⊥圆o所在平面,CD在圆o所在平面内,
∴PA⊥CD,
∵PA∩AB=A,∴CD⊥平面PAB,
∴PB⊥CD.
(Ⅱ)解:过点A作PB的垂线,过点H作PB的垂线,分别交PB于点E,F;
∵Rt△PAB中,∠PBA=45°,PB=2
| 2 |
∴PA=AB=2,∴AE=ABsin45°=
| 2 |
又∵∠CAB=∠DAB=60°,∴AC=AD=1,
∵CH⊥AH,∴AH=
| 1 |
| 2 |
∴BH=
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
∴VH-PBD=VP-HDB=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 4 |
S△PBD=
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
∴H到平面PBD的距离为
| ||||
|
3
| ||
| 10 |
点评:本题考查了线面垂直的判定与性质定理,同时考查了利用体积求高的方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知R是实数集,M={x|
<1},N={y|y=
},则N∩∁R,N={y|y=
},则N∩∁RM( )
| 2 |
| x |
| x-1 |
| x-1 |
| A、(1,2) | B、[0,2] |
| C、CϕD | D、[1,2] |
 已知椭圆C:
已知椭圆C: