题目内容
1.对于每一个实数x,设f(x)是4x+1,x+2和4-2x三个函数中的最小值,则f(x)的最大值是( )| A. | $\frac{8}{3}$ | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
分析 求出f(x)的解析式,分段求最大值得出.
解答 解:解$\left\{\begin{array}{l}{4x+1<x+2}\\{4x+1<4-2x}\end{array}\right.$,得x$<\frac{1}{3}$,解$\left\{\begin{array}{l}{x+2<4x+1}\\{x+2<4-2x}\end{array}\right.$,得$\frac{1}{3}<x<\frac{2}{3}$,解$\left\{\begin{array}{l}{4-2x<4x+1}\\{4-2x<x+2}\end{array}\right.$,得x$>\frac{2}{3}$,
∴f(x)=$\left\{\begin{array}{l}{4x+1,x≤\frac{1}{3}}\\{x+2,\frac{1}{3}<x<\frac{2}{3}}\\{4-2x,x≥\frac{2}{3}}\end{array}\right.$,
当x$≤\frac{1}{3}$时,f(x)是增函数,fmax(x)=f($\frac{1}{3}$)=$\frac{7}{3}$,
当$\frac{1}{3}<x<\frac{2}{3}$时,f(x)是增函数,fmax(x)=f($\frac{2}{3}$)=$\frac{8}{3}$,
当x≥$\frac{2}{3}$时,f(x)是减函数,fmax(x)=f($\frac{2}{3}$)=$\frac{8}{3}$.
综上,f(x)的最大值是$\frac{8}{3}$.
故选:A.
点评 本题考查了分段函数最值的求法,求出f(x)的解析式是关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
12.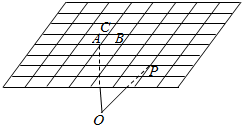 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )| A. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$ | B. | $\overrightarrow{OA}$-3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | C. | $\overrightarrow{OA}$+3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | D. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$-3$\overrightarrow{AC}$ |
15.如图,正方体中,两条异面直线BC1与B1D1所成的角是( )
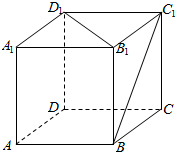

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
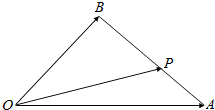 如图,在△AOB中,已知P为线段AB上的一点,且$\overrightarrow{BP}$=2$\overrightarrow{PA}$.
如图,在△AOB中,已知P为线段AB上的一点,且$\overrightarrow{BP}$=2$\overrightarrow{PA}$.